
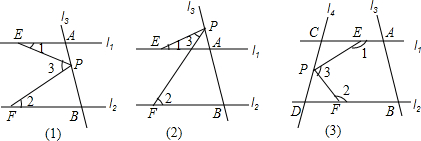
分析 此题三个小题的解题思路是一致的,过P作直线l1、l2的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.
解答 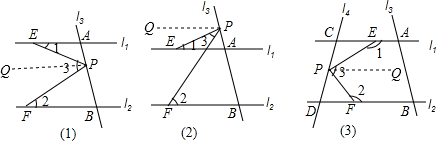 证明:(1)过P作PQ∥l1∥l2,
证明:(1)过P作PQ∥l1∥l2,
由两直线平行,内错角相等,可得:
∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPE+∠QPF,
∴∠3=∠1+∠2.
(2)关系:∠3=∠2-∠1;
过P作直线PQ∥l1∥l2,
则:∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPF-∠QPE,
∴∠3=∠2-∠1.
(3)关系:∠3=360°-∠1-∠2.
过P作PQ∥l1∥l2;
同(1)可证得:∠3=∠CEP+∠DFP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠CEP+∠DFP+∠1+∠2=360°,
即∠3=360°-∠1-∠2.
点评 此题主要考查的是平行线的性质,能够正确地作出辅助线,是解决问题的关键.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 当AB=BC时,?ABCD是菱形 | B. | 当∠ABC=90°时,?ABCD是矩形 | ||
| C. | 当AC⊥BD时,?ABCD是菱形 | D. | 当AC=BD时,?ABCD是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
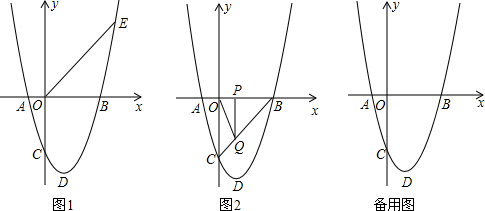
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
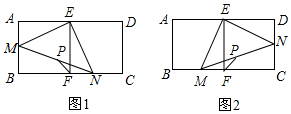
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
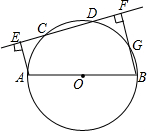 如图所示,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD交直线CD于点E,BF⊥CD交直线CD于点F,若BF交⊙O于G.求证:$\widehat{AC}$=$\widehat{DG}$.
如图所示,AB是⊙O的直径,CD是⊙O的弦,AE⊥CD交直线CD于点E,BF⊥CD交直线CD于点F,若BF交⊙O于G.求证:$\widehat{AC}$=$\widehat{DG}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com