
已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.
(1)求这条抛物线的解析式;
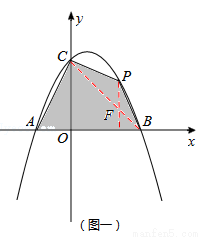
(2)如图一,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标;
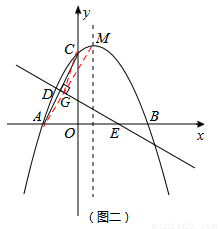
(3)如图二,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.

(1)y=﹣x2+x+2;(2)当点P坐标为(1,2)时,四边形ABPC的面积最大;(3)存在,点G的坐标为(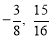 ).
).
【解析】
试题分析:(1)利用待定系数法即可求得.
(2)如答图1,四边形ABPC由△ABC与△PBC组成,△ABC面积固定,则只需要使得△PBC面积最大即可.求出△PBC面积的表达式,然后利用二次函数性质求出最值.
(3)如答图2,DE为线段AC的垂直平分线,则点A、C关于直线DE对称.连接AM,与DE交于点G,此时△CMG的周长=CM+CG+MG=CM+AM最小,故点G为所求.分别求出直线DE、AM的解析式,联立后求出点G的坐标.
试题解析:(1)∵抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、C(0,2)三点.
∴ , 解得
, 解得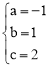 .
.
∴这条抛物线的解析式为:y=﹣x2+x+2.
(2)设直线BC的解析式为:y=kx+m,将B(2,0)、C(0,2)代入得:
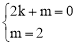 ,解得
,解得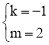 .
.
∴直线BC的解析式为:y=﹣x+2.
如答图1,连接BC.
四边形ABPC由△ABC与△PBC组成,△ABC面积固定,则只需要使得△PBC面积最大即可.
设P(x,﹣x2+x+2),
过点P作PF∥y轴,交BC于点F,则F(x,﹣x+2).
∴PF=(﹣x2+x+2)﹣(﹣x+2)=﹣x2+2x.
S△PBC=S△PFC+S△PFB=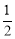 PF(xF﹣xC)+
PF(xF﹣xC)+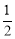 PF(xB﹣xF)=
PF(xB﹣xF)=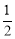 PF(xB﹣xC)=PF
PF(xB﹣xC)=PF
∴S△PBC=﹣x2+2x=﹣(x﹣1)2+1
∴当x=1时,△PBC面积最大,即四边形ABPC面积最大.此时P(1,2).
∴当点P坐标为(1,2)时,四边形ABPC的面积最大.
(3)存在.
∵∠CAO+∠ACO=90°,∠CAO+∠AED=90°,∴∠ACO=∠AED.
又∵∠CAO=∠CAO,∴△AOC∽△ADE.
∴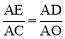 ,即
,即 ,解得AE=
,解得AE=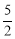 .
.
∴E(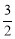 ,0).
,0).
∵DE为线段AC的垂直平分线,∴点D为AC的中点,∴D(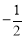 ,1).
,1).
可求得直线DE的解析式为: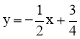 ①.
①.
∵ ,∴M(
,∴M(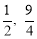 ).
).
又A(﹣1,0),则可求得直线AM的解析式为: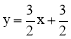 ②.
②.
∵DE为线段AC的垂直平分线,∴点A、C关于直线DE对称.
如答图2,连接AM,与DE交于点G,
此时△CMG的周长=CM+CG+MG=CM+AM最小,故点G为所求.
联立①②式,可求得交点G的坐标为(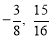 ).
).
∴在直线DE上存在一点G,使△CMG的周长最小,点G的坐标为(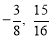 ).
).
考点:1.二次函数综合题;2.单击动点问题;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.二次函数的性质;6.线段垂直平分线的性质;7.轴对称的应用(最短线路问题).


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源:2014年初中毕业升学考试(甘肃天水卷)数学(解析版) 题型:填空题
天水市某校从三名男生和两名女生中选出两名同学做为“伏羲文化节”的志愿者,则选出一男一女的概率为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(甘肃兰州卷)数学(解析版) 题型:选择题
函数y=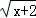 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x>﹣2 B.x≥﹣2 C.x≠2 D.x≤﹣2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南长沙卷)数学(解析版) 题型:选择题
下列计算正确的是( )
A. B.(ab2)2=ab4 C.2a+3a=6a D.a•a3=a4
B.(ab2)2=ab4 C.2a+3a=6a D.a•a3=a4
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南郴州卷)数学(解析版) 题型:解答题
我市党的群众路线教育实践活动不断推进并初见成效.某县督导小组为了解群众对党员干部下基层、查民情、办实事的满意度(满意度分为四个等级:A、非常满意;B、满意;C、基本满意;D、不满意),在某社区随机抽样调查了若干户居民,并根据调查数据绘制成下面两个不完整的统计图.

请你结合图中提供的信息解答下列问题.
(1)这次被调查的居民共有 户;
(2)请将条形统计图补充完整.
(3)若该社区有2000户居民,请你估计这个社区大约有多少户居民对党员干部的满意度是“非常满意”.根据统计结果,对党员干部今后的工作有何建议?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南邵阳卷)数学(解析版) 题型:解答题
小武新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南衡阳卷)数学(解析版) 题型:选择题
如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为( )

A.26米 B.28米 C.30米 D.46米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com