【题目】完成下面的证明.
已知：如图，
，
.
求证：
.
证明：∵，
∴
__________（_______________________________________）.
∴
（_____________________________________________）.
∵
，
∴_______
∴（______________________________________）.
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（6，6），将正方形ABCO绕点C逆时针旋转角度α（0°＜α＜90°），得到正方形CDEF，ED交线段AB于点G，ED的延长线交线段OA于点H，连CH、CG．
（1）求证：△CBG≌△CDG；
（2）求∠HCG的度数；并判断线段HG、OH、BG之间的数量关系，说明理由；
（3）连结BD、DA、AE、EB得到四边形AEBD，在旋转过程中，四边形AEBD能否为矩形？如果能，请求出点H的坐标；如果不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在如图所示的方格图中，我们称每个小正方形的顶点为“格点”，以格点为顶点的三角形叫做“格点三角形”，根据图形，回答下列问题.
（1）图中格点三角形A′B′C′是由格点三角形ABC通过怎样的平移得到的？
（2）如果以直线a，b为坐标轴建立平面直角坐标系后，点A的坐标为(－3，4)，请写出格点三角形DEF各顶点的坐标，并求出三角形DEF的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，铁路上A，B两点相距25 km，C，D为两村庄，DA⊥AB于点A，CB⊥AB于点B，已知DA＝16 km，CB＝11 km，现在要在铁路AB上建一个土特产品收购站E，使得C，D两村到E站的距离相等，则E站应建在离A站多少km处？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，抛物线
经过点A（﹣3，0）和点B（2，0）．直线
（
为常数，且
）与BC交于点D，与
轴交于点E，与AC交于点F．
（1）求抛物线的解析式；
（2）连接AE，求
为何值时，△AEF的面积最大；
（3）已知一定点M（﹣2，0）．问：是否存在这样的直线
，使△BDM是等腰三角形？若存在，请求出
的值和点D的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有A、B两个黑布袋，A布袋中有四个除标号外完全相同的小球，小球上分别标有数字0，1，2，3，B布袋中有三个除标号外完全相同的小球，小球上分别标有数字0，1，2．小明先从A布袋中随机取出一个小球，用m表示取出的球上标有的数字，再从B布袋中随机取出一个小球，用n表示取出的球上标有的数字．
（1）用（m，n）表示小明取球时m与n的对应值，画出树状图（或列表），写出（m，n）的所有取值；
（2）求关于x的一元二次方程
没有实数根的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=90°，点D是AB边上的一点，DM⊥AB，且DM=AC，过点M作ME∥BC交AB于点E，
（1）试说明△ABC与△MED全等；
（2）若∠M=35°，求∠B的度数？
查看答案和解析>>
科目：初中数学 来源： 题型：
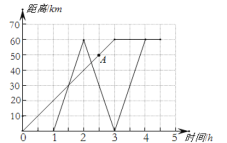
【题目】小南一家到某度假村度假．小南和妈妈坐公交车先出发，爸爸自驾车沿着相同的道路后出发．爸爸到达度假村后，发现忘了东西在家里，于是立即返回家里取，取到东西后又马上驾车前往度假村（取东西的时间忽略不计）．如下图是他们离家的距离s(km)与小南离家的时间t(h)的关系图．请根据图回答下列问题：
(1)图中的自变量是_________，因变量是_________，小南家到该度假村的距离是_____km．
(2)小南出发___________小时后爸爸驾车出发，爸爸驾车的平均速度为___________km/h，图中点A表示 ．
(3)小南从家到度假村的路途中，当他与爸爸相遇时,离家的距离约是___________km．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，点
在
边所在直线上（与点
，
不重合），点
在
边所在直线上，且
，
交
边于点
．
（1）如图1，若是等边三角形，点在边上，过点作
于
，试说明：
．
某同学发现可以由以下两种思路解决此问题：
思路一：过点作
，交于点
，如图1
因为是等边三角形，得
是等边三角形
又由，得
再说明
得出
．
从而得到结论．
思路二：过点作
，交的延长线于点
，如图
①请你在“思路一”中的括号内填写理由；
②根据“思路二”的提示，完整写出说明过程；
（2）如图3，若是等腰直角三角形，
，点在线段
的延长线上，过点作
于，试探究与
之间的数量关系，并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
