
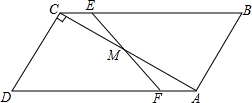
 ��ͼ����֪�ı���ABCD��ƽ���ı��Σ�ACΪ�Խ��ߣ���DAC=30�㣬��ACD=90�㣬AD=8����MΪAC���е㣬����E�ӵ�C������ÿ��1����λ���ٶ��˶�����Bֹͣ������EM���ӳ���AD�ڵ�F�����E���˶�ʱ��Ϊt�룮
��ͼ����֪�ı���ABCD��ƽ���ı��Σ�ACΪ�Խ��ߣ���DAC=30�㣬��ACD=90�㣬AD=8����MΪAC���е㣬����E�ӵ�C������ÿ��1����λ���ٶ��˶�����Bֹͣ������EM���ӳ���AD�ڵ�F�����E���˶�ʱ��Ϊt�룮���� ��1������ֱ����������30������Ե�ֱ�DZߵ���б�ߵ�һ�����ƽ���ı��εĶ��ߣ������õ׳��Ը��������
��2����ϡ�EMC=90���Լ�ƽ���ı��ε����ʣ���֤���ı���DCEF��ƽ���ı��Σ���ͨ������õ�ƽ���ı���CDFE��һ���ڱ���ȼ���֤�ý��ۣ�
��3��̽����BEMΪ���������Σ�Ҫ����������������ۣ�EB=EM��EB=BM��EM=BM��ͨ����Ӧ�ļ����ʾ��BE��EM��BM��Ȼ�����ñ���Ƚ������̽�����⣮
��� �⣺��1���ߡ�DAC=30�㣬��ACD=90�㣬AD=8��
��CD=4��AC=4$\sqrt{3}$��
�֡��ı���ABCDΪƽ���ı��Σ�
���ı���ABCD�����Ϊ4��4$\sqrt{3}$=16$\sqrt{3}$��
��2����ͼ1������EMC=90��ʱ���ı���DCEF�����Σ�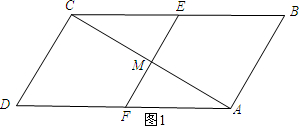
�ߡ�EMC=��ACD=90�㣬
��DC��EF��
��BC��AD��
���ı���DCEF��ƽ���ı��Σ���BCA=��DAC
���ɣ�1����֪��CD=4��AC=4$\sqrt{3}$��
�ߵ�MΪAC���е㣬
��CM=2$\sqrt{3}$��
��Rt��EMC�У���CME=90�㣬��BCA=30�㣮
��CE=2ME���ɵ�ME2+��2$\sqrt{3}$��2=��2ME��2��
��ã�ME=2��
��CE=2ME=4��
��CE=DC��
�֡��ı���DCEF��ƽ���ı��Σ�
���ı���DCEF�����Σ�
��3����E���˶���������ʹ��BEMΪ���������Σ�
���ɣ���ͼ2������B��BG��AD���G������E��EH��AD�ڵ�H������DM��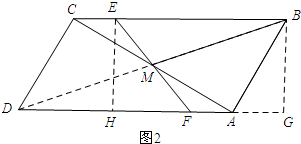
��DC��AB����ACD=90�㣬
���CAB=90�㣮
���BAG=180��-30��-90��=60�㣮
���ABG=30�㣮
��AG=$\frac{1}{2}AB$=2��BG=2$\sqrt{3}$��
�ߵ�E���˶��ٶ�Ϊÿ��1����λ���˶�ʱ��Ϊt�룬
��CE=t��BE=8-t��
�ڡ�CEM�͡�AFM��$\left\{\begin{array}{l}{��BCM=��MAF}\\{MC=AM}\\{��CME=��AMF}\end{array}\right.$��
���CEM�ա�AFM��
��ME=MF��CE=AF=t��
��HF=HG-AF-AG=BE-AF-AG=8-t-2-t=6-2t��
��EH=BG=2$\sqrt{3}$��
����Rt��EHF��ME=$\frac{1}{2}EF$=$\frac{1}{2}\sqrt{E{H}^{2}+H{F}^{2}}$=$\frac{1}{2}\sqrt{12+��6-2t��^{2}}$��
��MΪƽ���ı���ABCD�Խ���AC���е㣬
��D��M��B���ߣ���DM=BM��
����Rt��DBG��DG=AD+AG=10��BG=2$\sqrt{3}$��
��BM=$\frac{1}{2}��4\sqrt{7}$=2$\sqrt{7}$��
Ҫʹ��BEMΪ���������Σ�Ӧ���������������
��EB=EMʱ����$��8-t��^{2}=\frac{1}{4}[12+��6-2t��^{2}]$��
��ã�t=5.2��
��EB=BMʱ����8-t=2$\sqrt{7}$��
��ã�t=8-2$\sqrt{7}$��
��EM=BMʱ���������֪��E���B�غϣ���ʱ��B��E��M�����������Σ�
������������t=5.2��t=8-2$\sqrt{7}$ʱ����BEMΪ���������Σ�
���� ������Ҫ�������ƽ���ı��ε����ʡ����ε����ʺ��ж���ȫ�������ε����ʺ��ж�����30��ֱ�������ε����ʡ����������ε����ʡ����ɶ�����Ӧ�ã����������EB=EM��EB=BM��EM=BM�����ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.1����ȷ��ʮ��λ�� | B�� | 0.05����ȷ��ǧ��λ�� | ||
| C�� | 0.05����ȷ��0.01�� | D�� | 0.052����ȷ��0.001�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��502�����ε���� | B�� | ��502�����ε��ұ� | ||
| C�� | ��504�����ε���� | D�� | ��503�����ε��ұ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
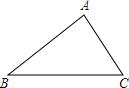 ��ͼ�������������ABC�У�AB=10��AC=2$\sqrt{13}$��sinB=$\frac{3}{5}$��
��ͼ�������������ABC�У�AB=10��AC=2$\sqrt{13}$��sinB=$\frac{3}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | 32007 | D�� | -32007 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
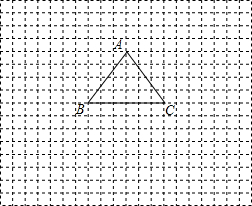 ��ͼ������������ABC��AB=AC=5��BC=6��
��ͼ������������ABC��AB=AC=5��BC=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1 | B�� | 0 | C�� | 1 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
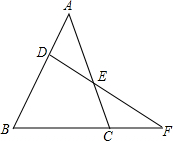 ��֪����ͼ��ABC�У�D��E�ֱ���AB��AC�ϵĵ㣬DE��BC���ӳ����ཻ��F��AD=CF����֤��$\frac{BC}{AB}$=$\frac{DE}{EF}$��
��֪����ͼ��ABC�У�D��E�ֱ���AB��AC�ϵĵ㣬DE��BC���ӳ����ཻ��F��AD=CF����֤��$\frac{BC}{AB}$=$\frac{DE}{EF}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com