
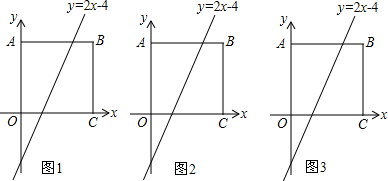
���� ��1�����������ֱ֪��y=2x-4��AB�Ľ����������Ϊ5����y=5����y=2x-4���ɵ�ֱ��y=2x-4��AB�Ľ���ĺ����꣬�Ӷ����ֱ��y=2x-4��AB�Ľ�������꣮
��2������������������D������Ϊ��p��q������D�ڵ�һ��������ֱ��y=2x-4�ϵ�һ�㣬�ɵ�p��q�Ĺ�ϵ����D�ڳ������ڲ��˶�ʱ���������߽磩����ͼ����Եõ�S��p�ĺ�����ϵʽ�Լ����m��ȡֵ��Χ��
��3���������֪����APD�ǵ��������η������������Ϊ��ĿҪ���ҵ�һ�����ɣ������ǿ����ȼ���һ�£�ͨ���ȽϿ�֪DA=DPʱ���Ƚ�������õ�D�����꣬��ѡ��������������
��� �⣺��1�����ڳ�����ABCO�У�OΪ����ԭ�㣬B������Ϊ��6��5����
��ֱ��y=2x-4��AB�Ľ����������Ϊ5��
��y=5����y=2x-4����
5=2x-4��
���x=4.5��
��ֱ��y=2x-4��AB�Ľ��������Ϊ��4.5��5����
��2�����D��������p��q����
��D�ڵ�һ��������ֱ��y=2x-4�ϵ�һ�㣬��D�ڳ������ڲ��˶����������߽磩��B������Ϊ��6��5����
��q=2p-4��
��${S}_{��ABD}=\frac{AB����BC-q��}{2}=\frac{6��[5-��2p-4��]}{2}$=3����5-2p+4��=3����9-2p��=27-6p��
��S=27-6p��
��y=0����y=2x-4����
x=2��
�֡�ֱ��y=2x-4��AB�Ľ��������Ϊ��4.5��5����
��2��p��4.5��
�ʵ�D�ڳ������ڲ��˶�ʱ���������߽磩��S��p�ĺ�����ϵʽΪ��S=27-6p��2��p��4.5��
��3�����D��������a��2a-4����
��P���߶�BC�ϵĶ��㣬��PC=m��
���P��������6��m����
����APD�ǵ��������Σ�
��DA=DPʱ��
�ߵ�A������Ϊ��0��5����D������Ϊ��a��2a-4������P������Ϊ��6��m����
�ࣨ2a-4-5��2+��a-0��2=��2a-4-m��2+��a-6��2��
��ã�a=$\frac{{m}^{2}+8m-3}{4m-8}$��
��2a-4=$\frac{{m}^{2}+13}{2m-4}$��
�ʵ�D������Ϊ����$\frac{{m}^{2}+8m-3}{4m-8}$��$\frac{{m}^{2}+13}{2m-4}$����
���� ���⿼��ֱ����ͼ��Ľ������⣬��������ȷ���Ա�����ȡֵ��Χ�������Ĺ�ϵʽ�����֪ʶ������ͼ�η�����ѡ����ʵ����������������⣬���������ε����֪ʶ���ѵ��ǽ�����еļ������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2����2$\frac{1}{3}$����-3����0 | B�� | ��-1��+��-$\frac{1}{3}$��+$\frac{1}{2}$��0 | C�� | ��-5��-|-5|+1��0 | D�� | |-1|����-2����0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
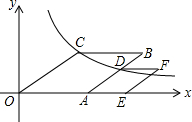 ��ͼ��������OABC�У���A����x�������ᣬ����������y=$\frac{k}{x}$��k��0��x��0����ͼ����C����AB���ڵ�D����ADΪһ������������AEFD����E����x���ϣ���֪��AOC=30�㣬OA•AE=12��������OABC�����������AEFD���������4$\sqrt{3}$��
��ͼ��������OABC�У���A����x�������ᣬ����������y=$\frac{k}{x}$��k��0��x��0����ͼ����C����AB���ڵ�D����ADΪһ������������AEFD����E����x���ϣ���֪��AOC=30�㣬OA•AE=12��������OABC�����������AEFD���������4$\sqrt{3}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com