
����Ŀ����֪���κ���y=x2��2x+c��c��0����ͼ����x�ύ��A��B���㣨A����B�����ࣩ����y�ύ�ڵ�C����OB=OC��
��������������ߵĽ���ʽ�Ͷ������ꣻ
������ֱ��l�������ߵĶԳ��ᣬE�������ߵĶ��㣬����BE���߶�OC�ϵĵ�F����ֱ��l�ĶԳƵ�F��ǡ�����߶�BE�ϣ����F�����ꣻ
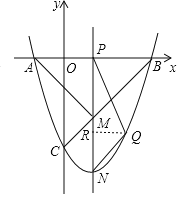
���������ж���P���߶�OB�ϣ�����P��x��Ĵ��߷ֱ���BC���ڵ�M���������߽��ڵ�N�����ʣ����������Ƿ���ڵ�Q��ʹ�á�PQN���APM�������ȣ����߶�NQ�ij�����С��������ڣ������Q�����ꣻ��������ڣ�˵�����ɣ�
���𰸡�����y=x2��2x��3����1����4����������F������Ϊ��0����2�������������ڣ���������ĵ�Q������Ϊ![]() ��
��![]() ��
��
��������������
��1������֪�����õ�C������Ϊ��0��c�������OB=OC����A�ڵ�B�����ɵõ�B������Ϊ��-c��0�����ѵ�B�����꣨-c��0������y=x2��2x+c�����c<0�������c��ֵ���Ӷ��õ������ߵĽ���ʽ�������ý���ʽ��Ϊ����ʽ���ɵõ������ߵĶ���������
��2���ɣ�1����֪�����ߵĶԳ���Ϊֱ��x=1�����F������Ϊ��0��m�������F�������Ϊ��2��m�����ɣ�1���ɵõ�B��E�����꣬���ɴ˿����ֱ��BE�Ľ���ʽ����F���������������BE�Ľ���ʽ�������m��ֵ���Ӷ��ɵô�ʱ��F�����ꣻ
��3������ͼ�����P������Ϊ��n��0������PA=n+1��PB=PM=3��n��PN=��n2+2n-3��
��QR��PN������ΪR����S��PQN=S��APM���ɵ�![]() ��n+1����3��n��=
��n+1����3��n��=![]() ����n2+2n+3��QR���������ɵ���QR=1��Ȼ��ֵ�Q��PN���Ҳ�������������ֱ��ú�n��ʽ�ӱ������R��N�����꣬Ȼ����Rt��QRN���ɹ��ɶ����ú�n��ʽ�ӱ����NQ2���������NQ��Сʱn��ֵ���ɴ˼��������Ӧ�ĵ�Q��������.
����n2+2n+3��QR���������ɵ���QR=1��Ȼ��ֵ�Q��PN���Ҳ�������������ֱ��ú�n��ʽ�ӱ������R��N�����꣬Ȼ����Rt��QRN���ɹ��ɶ����ú�n��ʽ�ӱ����NQ2���������NQ��Сʱn��ֵ���ɴ˼��������Ӧ�ĵ�Q��������.
��⣺
����y=x2��2x+c��c��0����
����C��������0��c����
��OB=OC����A�ڵ�B����࣬
����B����������c��0����
������c��0������y=x2��2x+c��
���c=��3��c=0����ȥ��
��c=��3��
�������ߵĽ���ʽΪy=x2��2x��3���䷽��y=��x��1��2��4��
������������1����4����
���������F��������0��m����
���Գ���Ϊֱ��l��x=1��
����F����ֱ�ߵĶԳƵ�F��������Ϊ��2��m����
��ֱ��BE�Ľ���ʽΪy=kx+b��
����1����֪��B��E������ֱ�Ϊ��3��0������1����4�����������������y=kx+b����
![]() �����
�����![]() ��
��
��ֱ��BE�Ľ���ʽΪy=2x��6��
����F����ֱ��BE�ϣ�
��m=2��2��6=��2��
����F��������0����2����
�����ڣ�
����ͼ��ʾ�����P������Ϊ��n��0����
��PA=n+1��PB=PM=3��n��PN=��n2+2n-3��
��QR��PN������ΪR��
��S��PQN=S��APM��
��![]() ��n+1����3��n��=
��n+1����3��n��=![]() ����n2+2n+3��QR��
����n2+2n+3��QR��
��QR=1��
����Q��ֱ��PN���Ҳ�ʱ��Q������Ϊ��n+1��n2��4����R�������Ϊ��n��n2��4����N�������Ϊ��n��n2��2n��3����
��QR=1��RN=2n-1��
����Rt��QNR��NQ2=1+��2n��1��2��
����n=![]() ʱ��NQȡ��Сֵ����ʱQ�������Ϊ
ʱ��NQȡ��Сֵ����ʱQ�������Ϊ![]() ��
��
����Q��ֱ��PN�����ʱ��Q�������Ϊ��n��1��n2��4n��
ͬ���ɵ���NQ2=1+��-2n+3��2��
����n=![]() ʱ��NQȡ��Сֵ����ʱQ�������Ϊ
ʱ��NQȡ��Сֵ����ʱQ�������Ϊ![]() ��
��
�������������������Q����Ϊ![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������:��a+b=2�����a��b�ǹ���1��ƽ����.
(1)ֱ����д:��3��_ �ǹ���1��ƽ����: :
��1-x��________�ǹ��� 1��ƽ����(�ú�x�Ĵ���ʽ��ʾ);
(2)��![]() ��
��![]() ,�Ȼ���a. b,���ж�a��b�Ƿ��ǹ���1��ƽ����.
,�Ȼ���a. b,���ж�a��b�Ƿ��ǹ���1��ƽ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�������������

(1)���ڢ��������еĹ��ɣ���7������____����![]() ������_______(�ú�
������_______(�ú�![]() ��ʽ�ӱ�ʾ)
��ʽ�ӱ�ʾ)
(2)�۲�ڢ�������ڢ������Ĺ�ϵ���ڢ��е�![]() ������________(�ú�
������________(�ú�![]() ��ʽ�ӱ�ʾ)
��ʽ�ӱ�ʾ)
�۲�ڢ�������ڢ������Ĺ�ϵ���ڢ��е�![]() ������__________(�ú�
������__________(�ú�![]() ��ʽ�ӱ�ʾ)
��ʽ�ӱ�ʾ)
(3)ȡÿ�����ĵ�8�������������������ĺ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڡ�ABC�͡�DBC�У���ACB=��DBC=90�㣬��E��BC���е㣬EF��AB������ΪF����AB=DE��
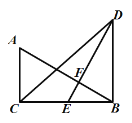
��1����֤����BCD�ǵ���ֱ�������Σ�
��2����BD=8���ף���AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
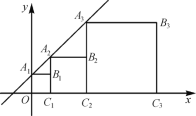
����Ŀ����������A1B1C1O��A2B2C2C1��A3B3C3C2����ͼ��ʾ��ʽ���ã���A1��A2��A3�����͵�C1��C2��C3�����ֱ���ֱ��![]() ��x���ϣ����B2019�ĺ�������______.
��x���ϣ����B2019�ĺ�������______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB��4 cm��BC��8 cm����P�ӵ�D�������A�˶����˶�����A��ֹͣ��ͬʱ��Q�ӵ�B�������C�˶����˶�����C��ֹͣ����P��Q���ٶȵ��ٶȶ���1 cm/s������PQ��AQ��CP�����P��Q�˶���ʱ��Ϊt(s)��
(1)��tΪ��ֵʱ���ı���ABQP�Ǿ��Σ�
(2)��tΪ��ֵʱ���ı���AQCP�����Σ�
(3)�ֱ����(2)������AQCP���ܳ��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��C��D��ֱ��AB�ϵ����㣬��1����2��180�㣬DEƽ�֡�CDF��EF��AB.
(1)���룺CE��DF�Ƿ�ƽ�У���˵�����ɣ�
(2)����DCE��130�㣬���DEF�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ո������һ��ѧϰ�ɼ����쵫����һ�������ͬѧδ����ѣ��Ѿ�Ϊ�����������п���������.����ĩ���ڼ���ϰ1������������ÿ����150��Ϊ������������IJ��ֱַ�������������ʾ��8�γɼ�����λ���£��ֱ��ǣ�10����8����5����2����2����8����3����4.
��1���ɼ���õ�һ�α�����һ�ζ��������£�
��2����������8��������ƽ���ɼ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
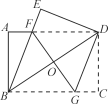
����Ŀ����ͼ1��������ֽƬABCD�ضԽ���BD�����۵�����C���ڵ�E����BE��AD�ڵ�F.
(1)��֤����BDF�ǵ��������Σ�
(2)��ͼ2������D��DG��BE����BC�ڵ�G������FG��BD�ڵ�O.
���ж��ı���BFDG����״����˵�����ɣ�
����AB��6��AD��8����FG�ij���
ͼ1
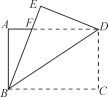
ͼ2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com