
【题目】观察下面三行数:

(1)按第①行数排列的规律,第7个数是____,第![]() 个数是_______(用含
个数是_______(用含![]() 的式子表示)
的式子表示)
(2)观察第②行数与第①行数的关系,第②行第![]() 个数是________(用含
个数是________(用含![]() 的式子表示)
的式子表示)
观察第③行数与第①行数的关系,第③行第![]() 个数是__________(用含
个数是__________(用含![]() 的式子表示)
的式子表示)
(3)取每行数的第8个数,计算这三个数的和.
【答案】(1)-128, ![]() ;(2)
;(2)![]() ,
, ![]() ;(3)573.
;(3)573.
【解析】
(1)发现前三个数的规律,依此计算第7个数及第n个数;(2) 观察发现第②行每个数都是第①行对应的数减3得到的,由此求得第②行第n个数;第③行每个数都是第①行对应的数除以4得到的,由此求得第③行第![]() 个数;(3)依据(1)、(2)的规律得到①②③行的第八个数相加即可.
个数;(3)依据(1)、(2)的规律得到①②③行的第八个数相加即可.
(1)第①行 第1个数是(-1)1![]() 2=-2
2=-2
第2个数是(-1)2![]() 2=4
2=4
第3个数是(-1)3![]() 23=-8
23=-8
……
第7个数是(-1)7![]() 27=-128
27=-128
第n个数是(-1)n![]() 2n
2n
(2) 第②行第1个数是-2-3=-5
第2个数是4-3=1
第3个数是-8-3=-11
……
第n个数是(-1)n![]() 2n-3
2n-3
第③行第1个数是-2![]() =
=![]()
第2个数是4![]() =1
=1
第3个数是-8![]() =-2
=-2
……
第n个数是(-1)n![]() 2n
2n![]() =(-1)n
=(-1)n![]()
(3)由(1)知第①行第8个数是28
由(2)知第②行第8个数是28-3,第③行第8个数是26
这三个数的和为28+28-3+26=256+256-3+64=573


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】(1)下面两个立体图形的名称是:__________,__________
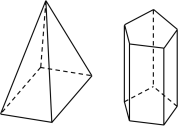
(2)一个立体图形的三视图如下图所示,这个立体图形的名称是__________

(3)画出下面立体图形的主视图.
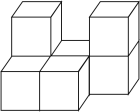
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分剪下,拼成右边的矩形,由图形①到图形②的变化过程能够验证的一个等式是( )
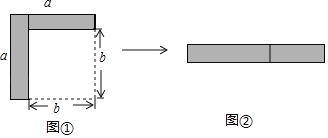
A. a(a+b)=a2+ab B. a2﹣b2=(a+b)(a﹣b)
C. (a+b)2=a2+2ab+b2 D. a(a﹣b)=a2﹣ab
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月第二届换广西公路自行车世界巡回赛开赛,有来自世界各地的多支顶级车队参赛,在本次赛事上,组委会把若干翻译志愿者分配给各车队.若毎支车队分配3人,则多出10人,若每支车队分配4人,则还缺8人.
(1)请问一共有几支车队参赛?
(2)组委会给每位参赛车手提供两张号码布和一个电子计时芯片,现有两家供应商提供了如下报价:
①若有![]() 名选手参赛,请用含
名选手参赛,请用含![]() 的式子分别表示甲、乙两家供应商所需的费用;
的式子分别表示甲、乙两家供应商所需的费用;
②请你通过计算说明组委会会选择哪个供应商比较省钱.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛自古就是中国的!2017年5月18日,中国海警2305,2308,2166,33115舰船队在中国的钓鱼岛领海内巡航,如图,我军以30km/h的速度在钓鱼岛A附近进行合法巡逻,当巡逻舰行驶到B处时,战士发现A在他的东北方向,巡逻舰继续向北航行40分钟后到达点C,发现A在他的东偏北15°方向,求此时巡逻舰与钓鱼岛的距离(![]() ≈1.414,结果精确到0.01)
≈1.414,结果精确到0.01)
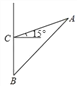
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴打车为市民的出行带来了很大的方便,小亮调查了若干市民一周内使用滴滴打车的时间t(单位:分),将获得的数据分成四组,绘制了如下统计图,请根据图中信息,解答下列问题:
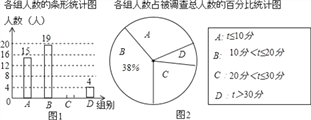
(1)这次被调查的总人数是多少?
(2)试求表示C组的扇形圆心角的度数,并补全条形统计图;
(3)若全市的总人数为666万,试求全市一周内使用滴滴打车超过20分钟的人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
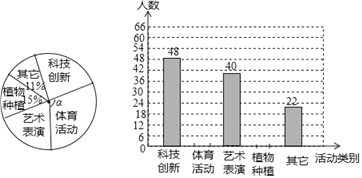
【题目】深圳市教育局在全市中小学开展“四点半活动”试点工作,某校为了了解学生参与“四点半活动”项目的情况,对初中的部分学生进行了随机调查,调查项目分为“科技创新”类,“体育活动”类,“艺术表演”类,“植物种植”类及“其它”类共五大类别,并根据调查的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息解答下面的问题.
(1)请求出此次被调查学生的总人数 人;
(2)根据以上信息,补全频数分布直方图;
(3)求出扇形统计图中,“体育活动”α的圆心角等于 度;
(4)如果本校初中部有1800名学生,请估计参与“艺术表演”类项目的学生大约多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x+c(c<0)的图象与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,且OB=OC.
(Ⅰ)求该抛物线的解析式和顶点坐标;
(Ⅱ)直线l是抛物线的对称轴,E是抛物线的顶点,连接BE,线段OC上的点F关于直线l的对称点F′恰好在线段BE上,求点F的坐标;
(Ⅲ)若有动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N,试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂制作甲、乙两种环保包装盒,已知同样用6m材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制成一个乙盒需要多用20%的材料.
(1)求制作每个甲盒、乙盒各用多少米材料?
(2)如果制作甲、乙两种包装盒共3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需要材料的总长度l(m)与甲盒数量n(个)之间的函数关系式,并求出最少需要多少米材料?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com