
分析 根据非负数的性质求出x、y,再利用积的乘方公式化简即可.
解答 解:∵13x2-6xy+y2-4x+1=0,
∴(9x2-6xy+y2)+(4x2-4x+1)=0
∴(3x-y)2+(2X-1)2=0,
∵(3x-y)2≥0,(2X-1)2≥0,
∴3x-y=0,x=$\frac{1}{2}$,
∴x=$\frac{1}{2}$,y=$\frac{3}{2}$,
∴x+y=2,
∴(x+y)2013•x2012=22013×($\frac{1}{2}$)2012=2×(2×$\frac{1}{2}$)2102=2.
点评 本题考查配方法的应用、非负数的性质、积的乘方公式,熟练掌握非负数的性质是解题的关键,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{7}+\sqrt{3}}{2}$ | B. | $\frac{\sqrt{7}-\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}-\sqrt{7}}{2}$ | D. | $\frac{-\sqrt{7}-\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
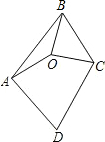 如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )
如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )| A. | 70° | B. | 110° | C. | 140° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
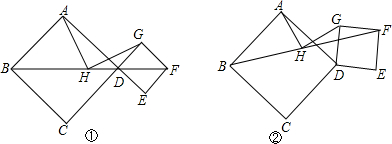
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com