【题目】如图,在平面内,两条直线L1,L2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线L1,L2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有_____个
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】弹簧挂上物体后会伸长，若一弹簧长度(cm)与所挂物体质量(kg)之间的关系如下表：
物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度(cm) | 12 | 12．5 | 13 | 13．5 | 14 | 14．5 |
则下列说法错误的是（ ）
A.弹簧长度随物体的质量的变化而变化，物体的质量是自变量，弹簧的长度是因变量
B.如果物体的质量为x kg，那么弹簧的长度y cm可以表示为y=12+0.5x
C.在弹簧能承受的范围内，当物体的质量为7kg时，弹簧的长度为16cm
D.在没挂物体时，弹簧的长度为12cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有一水果店，从批发市场按4元
千克的价格购进10吨苹果，为了保鲜放在冷藏室里，但每天仍有一些苹果变质，平均每天有50千克变质丢弃，且每存放一天需要各种费用300元，据预测，每天每千克价格上涨
元．
设x天后每千克苹果的价格为p元，写出p与x的函数关系式；
若存放x天后将苹果一次性售出，设销售总金额为y元，求出y与x的函数关系式；
该水果店将这批水果存放多少天后一次性售出，可以获得最大利润，最大利润为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，大树AB与大数CD相距13m，小华从点B沿BC走向点C，行走一段时间后他到达点E，此时他仰望两棵大树的顶点A和D，两条视线的夹角正好为90°，且EA=ED.已知大树AB的高为5m，小华行走的速度为1m/s，小华行走到点E的时间是（ ）
A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目：初中数学 来源： 题型：
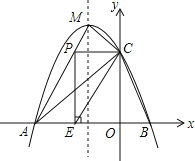
【题目】如图，抛物线
与x轴交于A、B两点，与y轴交于点
，且此抛物线的顶点坐标为
．
求此抛物线的解析式；
设点D为已知抛物线对称轴上的任意一点，当
与
面积相等时，求点D的坐标；
点P在线段AM上，当PC与y轴垂直时，过点P作x轴的垂线，垂足为E，将
沿直线CE翻折，使点P的对应点
与P、E、C处在同一平面内，请求出点坐标，并判断点是否在该抛物线上．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某农户发展养禽业，准备利用现有的34米长的篱笆靠墙AB（墙长为25米）围成一个面积为120平方米的长方形养鸡场，这个养鸡场的长和宽各是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，抛物线
经过点A（-3，4）．
（1）求b的值；
（2）过点A作
轴的平行线交抛物线于另一点B，在直线AB上任取一点P，作点A关于直线OP的对称点C；
①当点C恰巧落在
轴时，求直线OP的表达式；
②连结BC，求BC的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲于某日下午1时骑自行车从A地出发前往B地，乙于同日下午骑摩托车从A地出发前往B地，如图所示，图中折线PQR和线段MN分别表示甲和乙所行驶的路程和时间之间的关系图象，试根据图象回答下列问题．
（1）A、B两地相距多少千米？甲出发几小时，乙才开始出发？
（2）甲骑自行车的平均速度是多少？乙骑摩托车的平均速度是多少？
（3）乙在该日下午几时追上了甲？这时两人离B地还有多少千米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是-块长方形空地，长为
米，宽为
米，现要对其进行修整，在空白部分铺设
条宽度为
米的小路，其余阴影部分种植草坪．
（1）用整式表示小路的面积；
（2）用整式表示草坪的面积；
（3）现有两种修整方案，方案一：修建小路的宽度为
米；方案二：修建小路的宽度为米．铺设小路的造价为每平方米
元，种植草坪的造价为每平方米
元，请问选用哪种方案最划算．( 写出计算过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
