
【题目】郑州大学(ZhengzhouUniversity),简称“郑大”,是中华人民共和国教育部与河南省人民政府共建的全国重点大学,首批“双一流”世界一流大学、“211工程”.某学校兴趣小组3人来到郑州大学门口进行测量,如图,在大楼AC的正前方有一个舞台,舞台前的斜坡DE=4米,坡角∠DEB=41°,小红在斜坡下的点E处测得楼顶A的仰角为60°,在斜坡上的点D处测得楼顶A的仰角为45°,其中点B,C,E在同一直线上求大楼AC的高度.(结果精确到整数.参考数据:![]() ≈1.73,sin41°≈0.6,cos41°≈0.75,tan41°≈0.87)
≈1.73,sin41°≈0.6,cos41°≈0.75,tan41°≈0.87)

科目:初中数学 来源: 题型:
【题目】阅读下面材料后,解答问题.分母中含有未知数的不等式叫分式不等式.如:![]() ,
,![]() 等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知,两数相除,同号得正,异号得负,其字母表达式为:
等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知,两数相除,同号得正,异号得负,其字母表达式为:
(1)若![]() ,
,![]() ,则
,则![]() ,若
,若![]() ,
,![]() ,则
,则![]() ;
;
(2)若![]() ,
,![]() ,则
,则![]() ,若
,若![]() ,
,![]() ,则
,则![]() .反之,(1)若
.反之,(1)若![]() ,则
,则![]() 或
或![]()
(3)若![]() ,则__________或_____________.根据上述规律,求不等式
,则__________或_____________.根据上述规律,求不等式![]() ,的解集,方法如下:
,的解集,方法如下:
由上述规律可知,不等式![]() ,转化为①
,转化为①![]() 或②
或②![]()
解不等式组①得![]() ,解不等式组②得
,解不等式组②得![]() .
.
∴不等式![]() ,的解集是
,的解集是![]() 或
或![]() .
.
根据上述材料,解决以下问题:
A、求不等式![]() 的解集
的解集
B、乘法法则与除法法则类似,请你类比上述材料内容,运用乘法法则,解决以下问题:求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
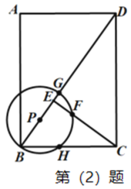
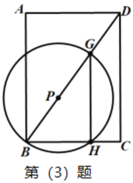
【题目】如图,在矩形 ABCD 中,CE⊥BD,AB=4,BC=3,P 为 BD 上一个动点,以 P 为圆心,PB 长半径作⊙P,⊙P 交 CE、BD、BC 交于 F、G、H(任意两点不重合),
(1)半径 BP 的长度范围为 ;
(2)连接 BF 并延长交 CD 于 K,若 tan KFC 3 ,求 BP;
(3)连接 GH,将劣弧 HG 沿着 HG 翻折交 BD 于点 M,试探究![]() 是否为定值,若是求出该值,若不是,请说明理由.
是否为定值,若是求出该值,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了践行“金山银山,不如绿水青山”的环保理念,重外环保小组的孩子们参与社区公益活动——收集废旧电池,活动开展一个月后,经过统计发现,全组成员平均每人收集了![]() 颗废旧电池,其中,收集数量低于
颗废旧电池,其中,收集数量低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,收集数量不低于
颗,收集数量不低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,数学王老师发现,若每人再多收集
颗,数学王老师发现,若每人再多收集![]() 颗,则收集数量低于
颗,则收集数量低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,收集数量不低于
颗,收集数量不低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,并且,该环保小组的人数介于
颗,并且,该环保小组的人数介于![]() 至
至![]() 人.则该环保小组有__________人.
人.则该环保小组有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,过二次函数y=﹣x2+4x图象上的点A(3,3)作x轴的垂线交x轴于点B.
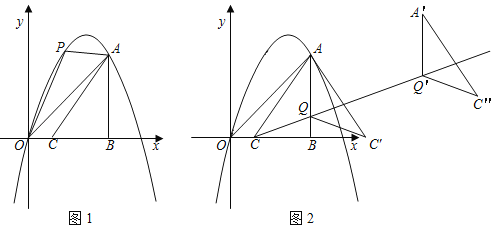
(1)如图1,P为线段OA上方抛物线上的一点,在x轴上取点C(1,0),点M、N为y轴上的两个动点,点M在点N的上方且MN=1.连接AC,当四边形PACO的面积最大时,求PM+MN![]() NO的最小值.
NO的最小值.
(2)如图2,点Q(3,1)在线段AB上,作射线CQ,将△AQC沿直线AB翻折,C点的对应点为C',将△AQC'沿射线CQ平移3![]() 个单位得△A'Q'C″,在射线CQ上取一点M,使得以A'、M、C″为顶点的三角形是等腰三角形,求M点的坐标.
个单位得△A'Q'C″,在射线CQ上取一点M,使得以A'、M、C″为顶点的三角形是等腰三角形,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
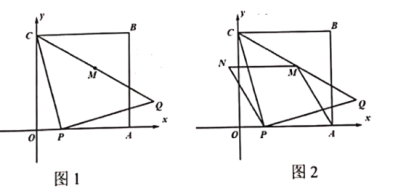
【题目】如图1,在平面直角坐标系中,正方形![]() 的边长为6,点
的边长为6,点![]() 分别在
分别在![]() 正半轴上,点
正半轴上,点![]() 在第一象限.点
在第一象限.点![]() 是
是![]() 正半轴上的一动点,且
正半轴上的一动点,且![]() ,连结
,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转90度至
顺时针旋转90度至![]() ,连结
,连结![]() ,取
,取![]() 中点
中点![]() .
.
(1)当![]() 时,求
时,求![]() 与
与![]() 的坐标.
的坐标.
(2)如图2,连结![]() ,以
,以![]() 、
、![]() 为邻边构造平行四边形
为邻边构造平行四边形![]() 记平行四边形
记平行四边形![]() 的面积为
的面积为![]() .
.
①用含![]() 的代数式表示
的代数式表示![]()
②当![]() 落在
落在![]() 的直角边上时,求
的直角边上时,求![]() 的度数.
的度数.
(3)在(2)的条件下,连结![]() ,记
,记![]() 的面积为
的面积为![]() ,若
,若![]() ,则
,则![]() (直接写出答案)
(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L1:y=﹣x2+bx+c经过点A(1,0)和点B(5,0)已知直线l的解析式为y=kx﹣5.
(1)求抛物线L1的解析式、对称轴和顶点坐标.
(2)若直线l将线段AB分成1:3两部分,求k的值;
(3)当k=2时,直线与抛物线交于M、N两点,点P是抛物线位于直线上方的一点,当△PMN面积最大时,求P点坐标,并求面积的最大值.
(4)将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方,将这部分图象与原抛物线剩余的部分组成的新图象记为L2
①直接写出y随x的增大而增大时x的取值范围;
②直接写出直线l与图象L2有四个交点时k的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 经过
经过![]() 三点,且
三点,且![]() .
.
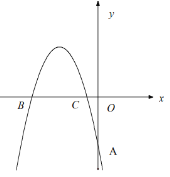
(1)求![]() 的值;
的值;
(2)在抛物线上求一点![]() 使得四边形
使得四边形![]() 是以
是以![]() 为对角线的菱形;
为对角线的菱形;
(3)在抛物线上是否存在一点![]() ,使得四边形
,使得四边形![]() 是以
是以![]() 为对角线的菱形?若存在,求出点
为对角线的菱形?若存在,求出点![]() 的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com