
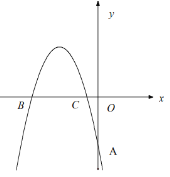
【题目】如图,在平面直角坐标系中,抛物线![]() 经过
经过![]() 三点,且
三点,且![]() .
.
(1)求![]() 的值;
的值;
(2)在抛物线上求一点![]() 使得四边形
使得四边形![]() 是以
是以![]() 为对角线的菱形;
为对角线的菱形;
(3)在抛物线上是否存在一点![]() ,使得四边形
,使得四边形![]() 是以
是以![]() 为对角线的菱形?若存在,求出点
为对角线的菱形?若存在,求出点![]() 的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)D
;(2)D![]() ;(3)存在,
;(3)存在,![]() ,这个菱形不是正方形.
,这个菱形不是正方形.
【解析】
(1)把A(0,-4)代入可求c,运用两根关系及x2-x1=5,对式子合理变形,求b;
(2)因为菱形的对角线互相垂直平分,故菱形的另外一条对角线必在抛物线的对称轴上,满足条件的D点,就是抛物线的顶点;
(3)根据四边形BPOH是以OB为对角线的菱形,可得PH垂直平分OB,求出OB的中点坐标,代入抛物线解析式即可,再根据所求点的坐标与线段OB的长度关系,判断是否为正方形.
解:(1)![]() 抛物线
抛物线![]() 经过点
经过点![]()
![]()
又由题意可知,![]() 是方程
是方程![]() 的两个根,
的两个根,
![]() ,
,![]()
由已知得![]()
又![]()
![]()
![]()
解得![]() ,
,
当![]() 时,抛物线与
时,抛物线与![]() 轴的交点在
轴的交点在![]() 轴的正半轴上,不合题意,舍去.
轴的正半轴上,不合题意,舍去.
![]() ;
;
(2)∵四边形![]() 是以
是以![]() 为对角线的菱形,根据菱形的性质,点
为对角线的菱形,根据菱形的性质,点![]() 必在抛物线的对称轴上,
必在抛物线的对称轴上,
又![]()
![]() 拋物线的顶点
拋物线的顶点![]() 即为所求的点
即为所求的点![]() ;
;
(3)∵四边形![]() 是以
是以![]() 为对角线的菱形,点
为对角线的菱形,点![]() 的坐标为
的坐标为![]()
根据菱形的性质,
点![]() 必是直线
必是直线![]() 与抛物线
与抛物线![]() 的交点,
的交点,
![]() 当
当![]() 时,
时,![]()
![]() 在抛物线上存在一点
在抛物线上存在一点![]() ,使得四边形
,使得四边形![]() 为菱形.
为菱形.
四边形![]() 不能成为正方形,
不能成为正方形,
因为如果四边形![]() 为正方形,.点
为正方形,.点![]() 的坐标只能是
的坐标只能是![]() ,但这一点不在抛物线上.
,但这一点不在抛物线上.


科目:初中数学 来源: 题型:
【题目】郑州大学(ZhengzhouUniversity),简称“郑大”,是中华人民共和国教育部与河南省人民政府共建的全国重点大学,首批“双一流”世界一流大学、“211工程”.某学校兴趣小组3人来到郑州大学门口进行测量,如图,在大楼AC的正前方有一个舞台,舞台前的斜坡DE=4米,坡角∠DEB=41°,小红在斜坡下的点E处测得楼顶A的仰角为60°,在斜坡上的点D处测得楼顶A的仰角为45°,其中点B,C,E在同一直线上求大楼AC的高度.(结果精确到整数.参考数据:![]() ≈1.73,sin41°≈0.6,cos41°≈0.75,tan41°≈0.87)
≈1.73,sin41°≈0.6,cos41°≈0.75,tan41°≈0.87)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一横截面是一抛物线的水渠.一次,水渠管理员将一根长![]() 的标杆一端放在水渠底部的
的标杆一端放在水渠底部的![]() 点,另一端露出水面并靠在水渠边缘的
点,另一端露出水面并靠在水渠边缘的![]() 点,发现标杆有
点,发现标杆有![]() 浸没在水中,露出水面部分的标杆与水面成
浸没在水中,露出水面部分的标杆与水面成![]() 的夹角(标杆与抛物线的横截面在同一平面内).
的夹角(标杆与抛物线的横截面在同一平面内).

(1)以水面所在直线为![]() 轴,建立如图所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号);
轴,建立如图所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号);
(2)在(1)的条件下,求当水面再上升![]() 时的水面宽约为多少?(
时的水面宽约为多少?(![]() 取
取![]() ,结果精确到
,结果精确到![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
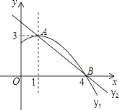
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: ①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,
其中正确的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
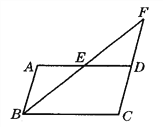
【题目】如图,平行四边形ABCD中,点E是AD的中点,BE的延长线与CD的延长线交于点F.
(1)求证:△ABE≌△DFE;
(2)试连结BD,AF,判断四边形ABDF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知网格的小正方形的边长均为1,格点三角形ABC如图所示,请用没有刻度的直尺画出满足条件的图形
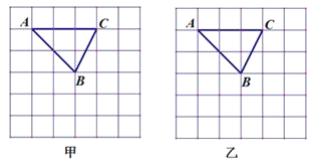
(1)在甲图中,画出△![]() ,且相似比为2:1,各顶点都在格点上.
,且相似比为2:1,各顶点都在格点上.
(2)在乙图中,把线段AB三等分.
查看答案和解析>>
科目:初中数学 来源: 题型:
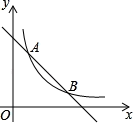
【题目】已知反比例函数y=![]() 与一次函数y=ax+b的图象相交于点A(2,6),和点B(4,m).
与一次函数y=ax+b的图象相交于点A(2,6),和点B(4,m).
(1)求反比例函数与一次函数的解析式;
(2)直接写出不等式![]() ≤ax+b的解集和△AOB的面积.
≤ax+b的解集和△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
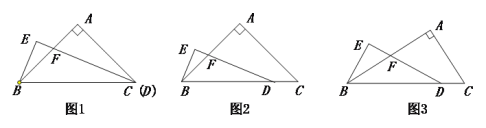
探究:当AB=AC且C,D两点重合时(如图1)探究:
(1)线段BE与FD之间的数量关系,直接写出结果 ;
(2)∠EBF= .
证明:当AB=AC且C,D不重合时,探究线段BE与FD的数量关系,并加以证明.
计算:当AB=![]() AC时,如图,求
AC时,如图,求![]() 的值 (用含
的值 (用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
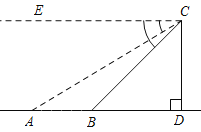
【题目】如图,直升飞机在大桥AB上方C点处测得A,B两点的俯角分别为45°和31°.若飞机此时飞行高度CD为1205m,且点A,B,D在同一条直线上,求大桥AB的长.(精确到1m)(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com