
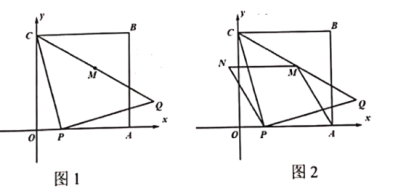
【题目】如图1,在平面直角坐标系中,正方形![]() 的边长为6,点
的边长为6,点![]() 分别在
分别在![]() 正半轴上,点
正半轴上,点![]() 在第一象限.点
在第一象限.点![]() 是
是![]() 正半轴上的一动点,且
正半轴上的一动点,且![]() ,连结
,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转90度至
顺时针旋转90度至![]() ,连结
,连结![]() ,取
,取![]() 中点
中点![]() .
.
(1)当![]() 时,求
时,求![]() 与
与![]() 的坐标.
的坐标.
(2)如图2,连结![]() ,以
,以![]() 、
、![]() 为邻边构造平行四边形
为邻边构造平行四边形![]() 记平行四边形
记平行四边形![]() 的面积为
的面积为![]() .
.
①用含![]() 的代数式表示
的代数式表示![]()
②当![]() 落在
落在![]() 的直角边上时,求
的直角边上时,求![]() 的度数.
的度数.
(3)在(2)的条件下,连结![]() ,记
,记![]() 的面积为
的面积为![]() ,若
,若![]() ,则
,则![]() (直接写出答案)
(直接写出答案)
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,②
,②![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)过点Q作![]() 轴于点D,首先证明
轴于点D,首先证明![]() ,则有
,则有![]() ,进而可求出点F的坐标,再结合点C的坐标,即可求出M的坐标;
,进而可求出点F的坐标,再结合点C的坐标,即可求出M的坐标;
(2)①根据(1)中的全等三角形的性质得出M的坐标,然后利用![]() 即可求出答案;
即可求出答案;
②分两种情况:当N在PC上时和当N在PQ上时,分别利用全等三角形的性质和等腰直角三角形的性质求出∠CPM和∠MPA的度数,然后利用两角的和与差即可得出答案;
(3)过点M作![]() 轴于点H,过点Q作
轴于点H,过点Q作![]() 轴于点G,然后用含t的代数式表示出
轴于点G,然后用含t的代数式表示出![]() ,然后分两种情况:点P在A点左侧和点P在A点右侧,分别建立关于t的一元二次方程求解即可.
,然后分两种情况:点P在A点左侧和点P在A点右侧,分别建立关于t的一元二次方程求解即可.
(1)过点Q作![]() 轴于点D,
轴于点D,

∵![]() ,
,
![]() .
.
∵正方形边长为6,
![]() ,
,
![]() .
.
由旋转的性质得,![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ;
;
(2)![]() ,
,
![]() ,
,
![]() .
.
∵C(0,6),
∴M![]() .
.
①当![]() 时,
时,![]() ;
;
②当N在PC上时,
∵点M的横纵坐标相等,
∴点M在对角线OB上,
连结OM,
在![]() 和
和![]() 中,
中,
![]()
∴CM=AM.
在Rt△CPQ中,M为CQ的中点,
∴PM⊥CQ,∠CPM=∠MPQ=45°,PM=CM=MQ,
∴PM=AM.
∵点N在PC上,NP∥AM,∠CPQ=90°,
∴AM⊥PQ,
∴∠PMA=45°,又PM=AM,
∴∠MPA=![]() ,
,
∴∠CPA=45°+67.5°=112.5°;
当N在PQ上时,同理可证MA=MP,∠AMP=45°,
∴∠MPA=![]() ,
,
∴∠CPA=67.5-45=22.5°,
综上所述,当点N在△CPQ的直角边上时,∠CPA的度数为112.5°或22.5°;
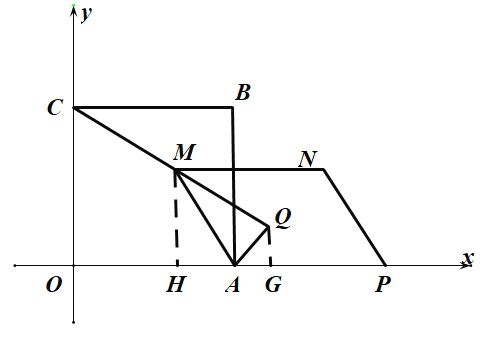
(3)过点M作![]() 轴于点H,过点Q作
轴于点H,过点Q作![]() 轴于点G,
轴于点G,
![]()
![]()
当![]() 时,即点P在A点左侧时,如图
时,即点P在A点左侧时,如图

![]() ,
,
![]() ,
,
解得![]() 或
或![]() (舍去);
(舍去);
当![]() 时,即点P在A点右侧时,
时,即点P在A点右侧时,
![]() ,
,
![]() ,
,
![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
综上所述,t的值为![]() 或
或![]() .
.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】广宇、承义两名同学分别进行5次射击训练,训练成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
广宇 | 9 | 8 | 7 | 7 | 9 |
承义 | 6 | 8 | 10 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A.广宇训练成绩的平均数大于承义训练成绩平均数
B.广宇训练成绩的中位数与承义训练成绩中位数不同
C.广宇训练成绩的众数与承义训练成绩众数相同
D.广宇训练成绩比承义训练成绩更加稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
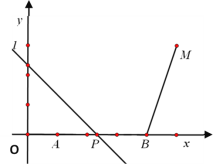
【题目】如图,点A(1, 0)、B(4,0)、M(5,3).动点P从A点出发,沿x轴以每秒1个单位的速度向右移动,过点P的直线l:y= -x+b也随之移动.设移动时间为t秒.
(1)当t=1时,求直线l的解析式.
(2)若直线l与线段BM有公共点,求t的取值范围.
(3)当点M关于直线l的对称点落在坐标轴上时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州大学(ZhengzhouUniversity),简称“郑大”,是中华人民共和国教育部与河南省人民政府共建的全国重点大学,首批“双一流”世界一流大学、“211工程”.某学校兴趣小组3人来到郑州大学门口进行测量,如图,在大楼AC的正前方有一个舞台,舞台前的斜坡DE=4米,坡角∠DEB=41°,小红在斜坡下的点E处测得楼顶A的仰角为60°,在斜坡上的点D处测得楼顶A的仰角为45°,其中点B,C,E在同一直线上求大楼AC的高度.(结果精确到整数.参考数据:![]() ≈1.73,sin41°≈0.6,cos41°≈0.75,tan41°≈0.87)
≈1.73,sin41°≈0.6,cos41°≈0.75,tan41°≈0.87)

查看答案和解析>>
科目:初中数学 来源: 题型:
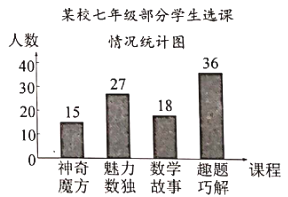
【题目】为培养学生数学学习兴趣,某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课(每位学生必须且只选其中一门).
(1)学校对七年级部分学生进行选课调查,得到如图所示的统计图.根据统计图,请估计该校七年级720名学生选“数学故事”的人数.
(2)学校将“数学故事”的学生分成人数相等的A,B,C三个班,小聪、小慧都选择了“数学故事”.已知小聪不在A班,求他与小慧被分到同一个班的概率.(要求列表或画树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020春开学为防控冠状病毒,学生进校园必须戴口罩,测体温,江阴初级中学开通了三条人工测体温的通道,每周一分别由王老师、张老师、李老师三位老师给进校园的学生测体温(每个通道一位老师),周一有小卫和小孙两学生进校园,在3个人工测体温通道中,可随机选择其中的一个通过.
(1) 求小孙进校园时,由王老师测体温的概率;
(2)求两学生进校园时,都是王老师测体温的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
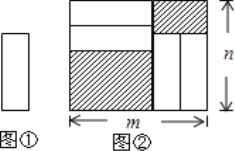
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一横截面是一抛物线的水渠.一次,水渠管理员将一根长![]() 的标杆一端放在水渠底部的
的标杆一端放在水渠底部的![]() 点,另一端露出水面并靠在水渠边缘的
点,另一端露出水面并靠在水渠边缘的![]() 点,发现标杆有
点,发现标杆有![]() 浸没在水中,露出水面部分的标杆与水面成
浸没在水中,露出水面部分的标杆与水面成![]() 的夹角(标杆与抛物线的横截面在同一平面内).
的夹角(标杆与抛物线的横截面在同一平面内).

(1)以水面所在直线为![]() 轴,建立如图所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号);
轴,建立如图所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号);
(2)在(1)的条件下,求当水面再上升![]() 时的水面宽约为多少?(
时的水面宽约为多少?(![]() 取
取![]() ,结果精确到
,结果精确到![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
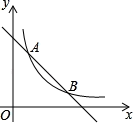
【题目】已知反比例函数y=![]() 与一次函数y=ax+b的图象相交于点A(2,6),和点B(4,m).
与一次函数y=ax+b的图象相交于点A(2,6),和点B(4,m).
(1)求反比例函数与一次函数的解析式;
(2)直接写出不等式![]() ≤ax+b的解集和△AOB的面积.
≤ax+b的解集和△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com