
����Ŀ��С���ﵥ����ѧ����������һ��·ʱ������Ҫ��ij���飬�������ۻص��վ�����ij��꣬��������ȥѧУ����������������ѧ���õ�ʱ����·�̵Ĺ�ϵʾ��ͼ������ͼ���ṩ����Ϣ�ش��������⣻
��1��С���ҵ�ѧУ��·������ ���ף�
��2��С���ۻ����ʱ�ﳵ���ٶ����� ����/�֣�С�������ͣ������ �����ӣ�
��3��������ѧ;�У�С��һ����ʻ���� ���ף������������ѧУһ�������� �����ӣ�
��4����������ѧ��;���� ���������� ������С���ﳵ�ٶ���죬�����ٶ����� ����/�֣�
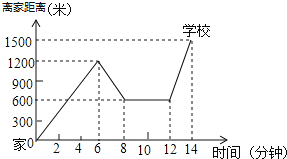
���𰸡���1��1500����2��300��4����3��2700��14����4��12��14��450
��������
��1�������������ʾ��Ҿ��룬�ɵ�С���ҵ�ѧУ��·�̣�
��2�������ۻ����ʱ��·�̳���ʱ�伴�����С���ۻ����ʱ�ﳵ���ٶȣ����������ʱ��Ҿ��벻�伴�ɵ�С�������ͣ����ʱ�䣻
��3�����С�������е�·�̣��ۻ�����·�̺ͼ���ȥѧУ���ߵ�·��֮�ͣ����ɵó�С��һ����ʻ��·�̣����ݺ������ʾʱ��ɵô����������ѧУһ���õ�ʱ�䣻
��4�����ݺ���ͼ��Խ��������С���ﳵ�ٶ���죬����·�̳���ʱ�伴����������ٶȣ�
�⣺����С��������ѧ���õ�ʱ����·�̵Ĺ�ϵʾ��ͼ��֪��
��1��С���ҵ�ѧУ��·����1500�ף�
�ʴ�Ϊ��1500��
��2��С���ۻ����ʱ�ﳵ���ٶ���![]() ��300����/�֣���
��300����/�֣���
С�������ͣ����12��8��4�����ӣ���
�ʴ�Ϊ��300��4��
��3��������ѧ;�У�С��һ����ʻ��1200+��1200��600��+��1500��600����2700�ף�
�����������ѧУһ������14���ӣ�
�ʴ�Ϊ��2700��14��
��4����������ѧ��;��12������14����С���ﳵ�ٶ���죬
�����ٶ���![]() ��450����/�֣���
��450����/�֣���
�ʴ�Ϊ��12��14��450��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У���ACB��90����AC��BC��ֱ��l������C��BD��l��AE��l��������ֱ�ΪD��E��
��1����A��B��ֱ��lͬ��ʱ����ͼ1��
��֤������AEC����CDB��
����AE=3,BD=4,�����ACB�����.(��ʾ�������)
(2)��A. B��ֱ��l����ʱ����ͼ2����AE=3��BD=4������AD��BEֱ��д������ADBE�����___.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
�У�![]() ��С��ͬѧ����ֱ�ߺ�Բ����������²�����
��С��ͬѧ����ֱ�ߺ�Բ����������²�����
����![]() ��ƽ����
��ƽ����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
������![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��
������![]() ��
��![]() .
.
����۲�ͼ�ν���������⣺

��1���߶�![]() ��
��![]() ��
��![]() ֮���������ϵ��________��
֮���������ϵ��________��
��2����![]() ����
����![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ�ֱ����6�����ѵ����ѵ���ɼ�����λ���������±�
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | |
�� | 9 | 8 | 6 | 7 | 8 | 10 |
�� | 8 | 7 | 9 | 7 | 8 | 8 |
�����ǵ�ѵ���ɼ������·���������˵����ȷ���ǣ�������
A. ����ѵ���ɼ���ƽ������ͬ B. ����ѵ���ɼ�����λ����ͬ
C. ����ѵ���ɼ���������ͬ D. ����ѵ���ɼ��ķ��ͬ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и��⣻
��1��4��a3��4����3a6��2
��2����6xy��x��2y��
��3����9x2y��6xy2����3xy
��4����a+2b����a��2b������a+b��2
��5������12��0+2��2
��6��20182��2017��2019���ù�ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ϻ�ڵĻ��Ⱦٰ죬ij��Ϻ��ֳ��Ϊ�˷��Ӽ������ƣ�һ�����չ���10000kgС��Ϻ���ƻ���ֳһ��ʱ����ٳ��ۣ���֪ÿ����ֳ��Ϻ�ijɱ���ͬ������10����ܳɱ�Ϊ166000������30����ܳɱ�Ϊ178000Ԫ��������С��Ϻ����t��������Ϊakg�����۵���ΪyԪ/kg���������������Ԥ�⣬a��t�ĺ�����ϵΪa=![]() ��y��t�ĺ�����ϵ��ͼ��ʾ��
��y��t�ĺ�����ϵ��ͼ��ʾ��
��1����ÿ�����ֳ�ɱ�ΪmԪ���չ��ɱ�ΪnԪ����m��n��ֵ��
��2����y��t�ĺ�����ϵʽ��
��3�����������С��Ϻ����t���һ���Գ�����������ΪWԪ���ʸ���Ϻ��ֳ������С��Ϻ�����������һ���Գ����������������������Ƕ��٣�
���ܳɱ�=�����ܷ���+�չ��ɱ�������=�����ܶ�ܳɱ���
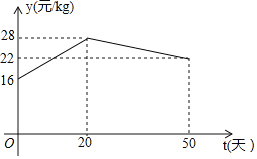
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱ���ABC�У���D��BC���ϣ������B����C�غϣ�����E��AC���ӳ����ϣ�DE=DA����ͼ1����
��1����֤����BAD=��EDC��
��2����E����ֱ��BC�ĶԳƵ�ΪM������DM��AM��
�������⽫ͼ2��ȫ��
������D��BC�����˶���DA��AMʼ���������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪,��ͼ, ��![]() ��,
��, ![]() ,
,![]() ,
,![]() ,P�DZ�BC�ϵ�һ���㣬����P��PE��AB,����ΪE���ӳ�PE����Q��ʹPQ=PC, ����
,P�DZ�BC�ϵ�һ���㣬����P��PE��AB,����ΪE���ӳ�PE����Q��ʹPQ=PC, ����![]() ����AB�ڵ�
����AB�ڵ�![]() .
.
��1����AD�ij���
��2����![]() ,
,![]() �����Ϊy, ��y����x�ĺ�������ʽ����д��������
�����Ϊy, ��y����x�ĺ�������ʽ����д��������
��3������C��![]() , ����ΪF, ����PF��QF, ��̽������P�ڱ�BC��ʲôλ��ʱ��
, ����ΪF, ����PF��QF, ��̽������P�ڱ�BC��ʲôλ��ʱ��![]() Ϊ�ȱ������Σ���ָ����P��λ�ò�����֤��.
Ϊ�ȱ������Σ���ָ����P��λ�ò�����֤��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������������ͼ��������и��⣺����ֱ��ͼ�������ۼ���
��1�����������ABC��������ڸ���ϣ�����ֱ��DE�ԳƵ���A1B1C1��
��2����DE�ϻ�����Q��ʹQA+QC��С��
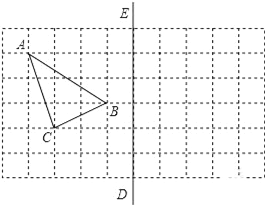
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com