
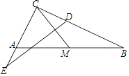
【题目】如图,点M是Rt△ABC的斜边AB的中点,连接CM,作线段CM的垂直平分线,分别交边CB和CA的延长线于点D、E,若∠C=90°,AB=20,tanB= ![]() ,则DE=________.
,则DE=________.
【答案】![]()
【解析】
设AC=2k,BC=5k,根据勾股定理得到AB=![]() k=20,得到BC=
k=20,得到BC=![]() ,连接DM,根据直角三角形的性质得到AM=CM=BM=
,连接DM,根据直角三角形的性质得到AM=CM=BM=![]() AB=10,由DE是线段CM的垂直平分线,得到CD=DM,根据相似三角形的性质得到CD=
AB=10,由DE是线段CM的垂直平分线,得到CD=DM,根据相似三角形的性质得到CD=![]() ,根据勾股定理得到DN=
,根据勾股定理得到DN=![]() =2,于是得到结论.
=2,于是得到结论.
∵∠C=90°,tanB=![]() ,
,
设AC=2k,BC=5k,
∴AB=![]() k=20,
k=20,
∴k=![]() ,
,
∴BC=![]() ,
,
连接DM,
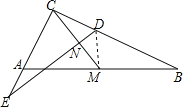
∵∠C=90°,点M是Rt△ABC的斜边AB的中点,
∴AM=CM=BM=![]() AB=10,
AB=10,
∴∠MCB=∠B,
∵DE是线段CM的垂直平分线,
∴CD=DM,
∴∠DCM=∠DMC,
∴△CDM∽△CMB,
∴![]() ,
,
∴CD=![]() ,
,
∵DE垂直平分CM,
∴∠E+∠ECN=∠ECN+∠NCD=90°,
∴∠E=∠NCD,
∴△CDE∽△NDC,
∴![]() ,
,
∵DN=![]() =2,
=2,
∴DE=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
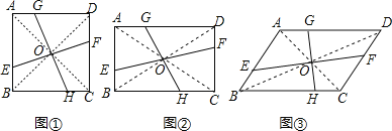
【题目】在四边形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交边AB、CD、AD、BC于点E、F、G、H
(感知)如图①,若四边形ABCD是正方形,且EF⊥GH,易知S△BOE=S△AOG,又因为S△AOB=![]() S四边形ABCD,所以S四边形AEOG=
S四边形ABCD,所以S四边形AEOG=![]() S正方形ABCD(不要求证明);
S正方形ABCD(不要求证明);
(拓展)如图②,若四边形ABCD是矩形,且S四边形AEOG=![]() S矩形ABCD,若AB=a,AD=b,BE=m,求AG的长(用含a、b、m的代数式表示);
S矩形ABCD,若AB=a,AD=b,BE=m,求AG的长(用含a、b、m的代数式表示);
(探究)如图③,若四边形ABCD是平行四边形,且S四边形AEOG=![]() SABCD,若AB=3,AD=5,BE=1,则AG=______.
SABCD,若AB=3,AD=5,BE=1,则AG=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
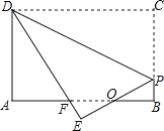
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE.、DE分别交AB于点O、F,且OP=OF,则BP的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6米,CD的长为6米,CD所在的水平线CG⊥EF于点G,铁塔EF的高为________米.(结果用带根号的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车由北京驶往相距840千米的沈阳,汽车的速度是每小时70千米,t小时后,汽车距沈阳s千米.
(1)求s与t的函数关系式,并写出自变量t的取值范围;
(2)经过2小时后,汽车离沈阳多少千米?
(3)经过多少小时后,汽车离沈阳还有140千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏思考解决如下问题:
原题:如图1,四边形ABCD中![]() ,
,![]() ,
,![]() 点P,Q分别在四边形ABCD的边BC,CD上,
点P,Q分别在四边形ABCD的边BC,CD上,![]() ,求证:
,求证:![]() .
.
![]() ______;
______;
![]() 小敏进行探索,如图2,将点P,Q的位置特殊化,使
小敏进行探索,如图2,将点P,Q的位置特殊化,使![]() ,
,![]() ,点E,F分别在边BC,CD上,此时她证明了
,点E,F分别在边BC,CD上,此时她证明了![]() 请你证明此时结论;
请你证明此时结论;
![]() 受以上
受以上![]() 的启发,在原题中,添加辅助线:如图3,作
的启发,在原题中,添加辅助线:如图3,作![]() ,
,![]() ,垂足分别为E,F,请你继续完成原题的证明.
,垂足分别为E,F,请你继续完成原题的证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
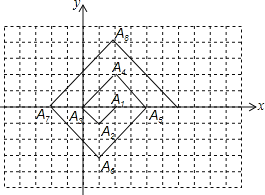
【题目】如图,在一个单位面积为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,……是斜边在x轴上,且斜边长分别为2,4,6,……的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,点A2019的横坐标为( )
A. 1010B. ![]() C. 1008D.
C. 1008D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.
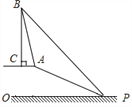
求:(1)坡顶A到地面PO的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com