
【题目】已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.
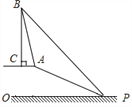
求:(1)坡顶A到地面PO的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
【答案】(1)10米;(2)19米.
【解析】试题分析:(1)先过点A作AH⊥PO,根据斜坡AP的坡度为1:2.4,得出![]() =
=![]() ,设AH=5k,则PH=12k,AP=13k,求出k的值即可;
,设AH=5k,则PH=12k,AP=13k,求出k的值即可;
(2)先延长BC交PO于点D,根据BC⊥AC,AC∥PO,得出BD⊥PO,四边形AHDC是矩形,再根据∠BPD=45°,得出PD=BD,然后设BC=x,得出AC=DH=x﹣14,最后根据在Rt△ABC中,tan76°=![]() ,列出方程,求出x的值即可.
,列出方程,求出x的值即可.
试题解析:解:(1)过点A作AH⊥PO,垂足为点H,
∵斜坡AP的坡度为1:2.4,∴![]() =
=![]() ,
,
设AH=5k,则PH=12k,由勾股定理,得AP=13k,
∴13k=26,解得k=2,
∴AH=10,
答:坡顶A到地面PQ的距离为10米.
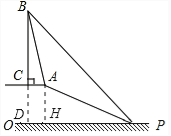
(2)延长BC交PO于点D,
∵BC⊥AC,AC∥PO,∴BD⊥PO,
∴四边形AHDC是矩形,CD=AH=10,AC=DH,
∵∠BPD=45°,∴PD=BD,
设BC=x,则x+10=24+DH,
∴AC=DH=x﹣14,
在Rt△ABC中,tan76°=![]() ,即
,即![]() ≈4.01.
≈4.01.
解得x≈19.
答:移动信号发射塔BC的高度约为19米.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
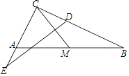
【题目】如图,点M是Rt△ABC的斜边AB的中点,连接CM,作线段CM的垂直平分线,分别交边CB和CA的延长线于点D、E,若∠C=90°,AB=20,tanB= ![]() ,则DE=________.
,则DE=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
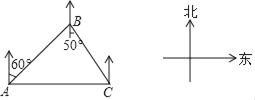
【题目】如图,淇淇一家驾车从A地出发,沿着北偏东60°的方向行驶,到达B地后沿着南偏东50°的方向行驶来到C地,C地恰好位于A地正东方向上,则( )
①B地在C地的北偏西50°方向上;
②A地在B地的北偏西30°方向上;
③cos∠BAC=![]() ;
;
④∠ACB=50°.其中错误的是( )
A. ①② B. ②④ C. ①③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量白塔的高度AB,在D处用高为1.5米的测角仪 CD,测得塔顶A的仰角为42°,再向白塔方向前进12米,又测得白塔的顶端A的仰角为61°,求白塔的高度AB.(参考数据sin42°≈0.67,tan42°≈0.90,sin61°≈0.87,tan61°≈1.80,结果保留整数)
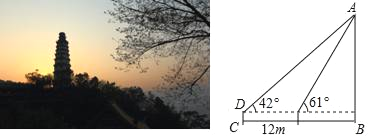
查看答案和解析>>
科目:初中数学 来源: 题型:
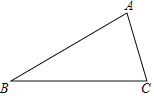
【题目】如图,在△ABC中,∠ACB=2∠B.
(1)作∠ACB的平分线交AB于D(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)若AB=10,AC=6,求△ACD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,![]() ,点
,点![]() .
.
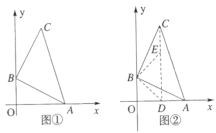
(1)在图①中,点![]() 坐标为__________;
坐标为__________;
(2)如图②,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,作等腰直角三角形
,作等腰直角三角形![]() ,
,![]() ,连接
,连接![]() .证明:
.证明:![]() ;
;
(3)在图②的条件下,若![]() 三点共线,求
三点共线,求![]() 的长;
的长;
(4)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 面积为2.请直接写出所有满足条件的点
面积为2.请直接写出所有满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你用直尺和圆规补全这个输水管道的圆形截面(保留作图痕迹);
(2)若这个输水管道有水部分的水面宽AB=8cm,水面最深地方的高度为2cm,求这个圆形截面的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com