
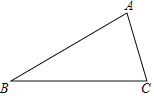
【题目】如图,在△ABC中,∠ACB=2∠B.
(1)作∠ACB的平分线交AB于D(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)若AB=10,AC=6,求△ACD的周长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小敏思考解决如下问题:
原题:如图1,四边形ABCD中![]() ,
,![]() ,
,![]() 点P,Q分别在四边形ABCD的边BC,CD上,
点P,Q分别在四边形ABCD的边BC,CD上,![]() ,求证:
,求证:![]() .
.
![]() ______;
______;
![]() 小敏进行探索,如图2,将点P,Q的位置特殊化,使
小敏进行探索,如图2,将点P,Q的位置特殊化,使![]() ,
,![]() ,点E,F分别在边BC,CD上,此时她证明了
,点E,F分别在边BC,CD上,此时她证明了![]() 请你证明此时结论;
请你证明此时结论;
![]() 受以上
受以上![]() 的启发,在原题中,添加辅助线:如图3,作
的启发,在原题中,添加辅助线:如图3,作![]() ,
,![]() ,垂足分别为E,F,请你继续完成原题的证明.
,垂足分别为E,F,请你继续完成原题的证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
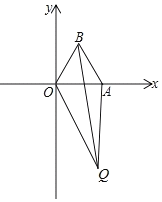
【题目】在平面直角坐标系中,O(0,0)、B(a,b),且a、b满足1﹣2a+a2+(b![]() )2=0.
)2=0.
(1)求a,b的值;
(2)若点A在x轴正半轴上,且OA=2,在平面内有一动点Q(不在x轴上),QO=m,QA=n,QB=p,且p2=m2+n2,求∠OQA的度数.
(3)阅读以下内容:对于实数a、b有(a﹣b)2≥0,∴a2﹣2ab+b2≥0,
即a2+b2≥2ab.
利用以上知识,在(2)的条件下求△AOQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在坡顶A处的同一水平面上有一座古塔BC,数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.
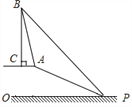
求:(1)坡顶A到地面PO的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
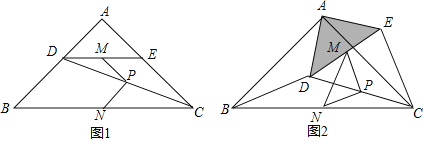
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过小学的学习我们知道,分数可分为“真分数”和“假分数”,并且假分数都可化为带分数.类比分数,对于分式也可以定义:对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).
如:![]()
解决下列问题:
(1)分式![]() 是________分式(填“真”或“假”);
是________分式(填“真”或“假”);
(2)假分式![]() 可化为带分式_________的形式;请写出你的推导过程;
可化为带分式_________的形式;请写出你的推导过程;
(3)如果分式![]() 的值为整数,那么
的值为整数,那么![]() 的整数值为_________.
的整数值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,顶点B的坐标为(4,6),直线y=kx+3k将平行四边形OABC分割成面积相等的两部分,则k的值是( ).

A.![]() B.
B.![]() C.-
C.-![]() D.﹣
D.﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=![]() x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
(1)求抛物线的解析式;
(2)若点D是线段BC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以B、C、E、P为顶点且以BC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com