
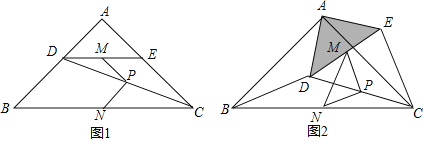
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
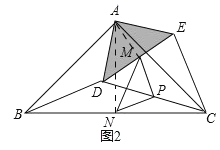
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
【答案】(1)PM=PN, PM⊥PN;(2)△PMN是等腰直角三角形,理由详见解析;(3)![]() .
.
【解析】
(1)利用三角形的中位线得出PM=![]() CE,PN=
CE,PN=![]() BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出结论;
BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线得出PM∥CE得出∠DPM=∠DCA,最后用互余即可得出结论;
(2)先判断出△ABD≌△ACE,得出BD=CE,同(1)的方法得出PM=![]() BD,PN=
BD,PN=![]() BD,即可得出PM=PN,同(1)的方法即可得出结论;
BD,即可得出PM=PN,同(1)的方法即可得出结论;
(3)方法1、先判断出MN最大时,△PMN的面积最大,进而求出AN,AM,即可得出MN最大=AM+AN,最后用面积公式即可得出结论.
方法2、先判断出BD最大时,△PMN的面积最大,而BD最大是AB+AD=14,即可.
解:(1)∵点P,N是BC,CD的中点,
∴PN∥BD,PN=![]() BD,
BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=![]() CE,
CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∵PN∥BD,
∴∠DPN=∠ADC,
∵PM∥CE,
∴∠DPM=∠DCA,
∵∠BAC=90°,
∴∠ADC+∠ACD=90°,
∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,
∴PM⊥PN,
故答案为:PM=PN,PM⊥PN,
(2)由旋转知,∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,BD=CE,
同(1)的方法,利用三角形的中位线得,PN=![]() BD,PM=
BD,PM=![]() CE,
CE,
∴PM=PN,
∴△PMN是等腰三角形,
同(1)的方法得,PM∥CE,
∴∠DPM=∠DCE,
同(1)的方法得,PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC
=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC
=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=90°,
∴∠ACB+∠ABC=90°,
∴∠MPN=90°,
∴△PMN是等腰直角三角形,
(3)方法1、如图2,同(2)的方法得,△PMN是等腰直角三角形,
∴MN最大时,△PMN的面积最大,
∴DE∥BC且DE在顶点A上面,
∴MN最大=AM+AN,
连接AM,AN,
在△ADE中,AD=AE=4,∠DAE=90°,
∴AM=2![]() ,
,
在Rt△ABC中,AB=AC=10,AN=5![]() ,
,
∴MN最大=2![]() +5
+5![]() =7
=7![]() ,
,
∴S△PMN最大=![]() PM2=
PM2=![]() ×
×![]() MN2=
MN2=![]() ×(7
×(7![]() )2=
)2=![]() .
.
方法2、由(2)知,△PMN是等腰直角三角形,PM=PN=![]() BD,
BD,
∴PM最大时,△PMN面积最大,
∴点D在BA的延长线上,
∴BD=AB+AD=14,
∴PM=7,
∴S△PMN最大=![]() PM2=
PM2=![]() ×72=
×72=![]()


科目:初中数学 来源: 题型:
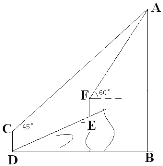
【题目】如图,在一次数学课外实践活动中,要求测量山坡前某建筑物的高度AB.小刚在D处用高1.5m的测角仪CD,测得该建筑物顶端A的仰角为45°,然后沿倾斜角为30°的山坡向上前进20m到达E,重新安装好测角仪后又测得该建筑物顶端A的仰角为60°.求该建筑物的高度AB.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC为等边三角形,O为BC的中点,D、E分别在边AB、AC上.如图1.
(1)若∠DOE=120°,求证:OD=OE;
(2)如图2,BD=4,CE=2,M是DE的中点,求OM的长.
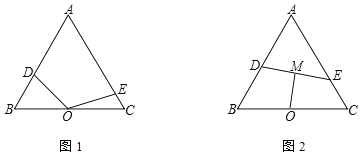
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)

查看答案和解析>>
科目:初中数学 来源: 题型:
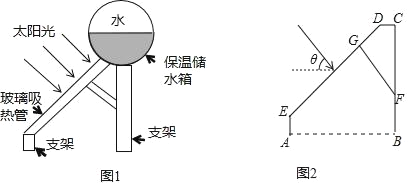
【题目】图1是太阳能热水器装置的示意图,利用玻璃吸热管可以把太阳能转化为热能,玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最好,假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光线与玻璃吸热管垂直),请完成以下计算:如图2,AB⊥BC,垂足为点B,CD∥AB,FG⊥DE,垂足为点G,若∠θ=37°50′,FG=30cm,CD=10cm,求CF的长(结果取整数,参考数据:sin37°50′≈0.6l,cos37°50′≈079,tan37°50′≈0.78)
查看答案和解析>>
科目:初中数学 来源: 题型:
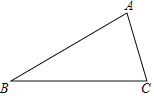
【题目】如图,在△ABC中,∠ACB=2∠B.
(1)作∠ACB的平分线交AB于D(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)若AB=10,AC=6,求△ACD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】讲授“轴对称”时,八年级教师设计了如下:四种教学方法:
① 教师讲,学生听
② 教师让学生自己做
③ 教师引导学生画图发现规律
④ 教师让学生对折纸,观察发现规律,然后画图
为调查教学效果,八年级教师将上述教学方法作为调研内容发到全年级8个班420名同学手中,要求每位同学选出自己最喜欢的一种.他随机抽取了60名学生的调查问卷,统计如图
(1) 请将条形统计图补充完整;
(2) 计算扇形统计图中方法③的圆心角的度数是 ;
(3) 八年级同学中最喜欢的教学方法是哪一种?选择这种教学方法的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图.对称轴x=﹣1.下列结论:
①4ac﹣b2<0;②4a+c<2b;③3b+2c<0.
其中正确结论的个数是( )

A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国制造”是世界上认知度最高的标签之一,因此,我县越来越多的群众选择购买国产空调,已知购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元,求A、B两种型号的空调的购买价各是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com