
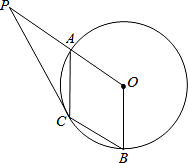
如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.
科目:初中数学 来源: 题型:
南博汽车城销售某种型号的汽车,每辆车的进货价为25万元.市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆,如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价-进货价)
(1)求y与x的函数关系式,在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
如果一个直角三角形的两条直角边AB=8 cm,BC=6 cm,若以点B为圆心,以某一直角边长为半径画圆,则 ( )
A.若点A在⊙B上,则点C在⊙B外
B.若点C在⊙B上,则点A在⊙B外
C.若点A在⊙B上,则点C在⊙B上
D.以上都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
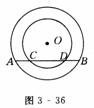
.如图3-36所示,在同心圆中,大圆的弦AB交小圆于C,D,已知AB=2CD,AB的弦心距等于CD长的一半 ,那么大圆与小圆的半径之比
,那么大圆与小圆的半径之比 是 ( )
是 ( )
A.3∶2 B.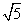 ∶2
∶2
C.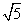 ∶
∶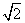 D.5∶4
D.5∶4
查看答案和解析>>
科目:初中数学 来源: 题型:
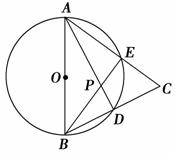
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE、AD交于点P.求证:
(1)D是BC的中点;
(2)△BEC∽△ADC.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
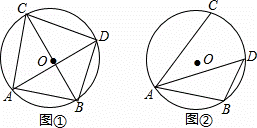
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
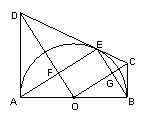
如图,已知AB为⊙O的直径,AD、BC、 CD为⊙O的切线,切点分别是A、B、E,则有一下结论:(1)CO⊥DO;(2)四边形OFEG是矩形.试说明理由.
CD为⊙O的切线,切点分别是A、B、E,则有一下结论:(1)CO⊥DO;(2)四边形OFEG是矩形.试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com