
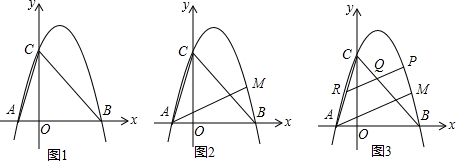
分析 (1)通过抛物线求出点AB坐标,利用等腰直角三角形性质求出C点坐标,代入抛物线即可求出a值;
(2)过点D做DE⊥AC交AC于点E,利用∠CAM=45°,表示线段EC长度,构造相似三角形,求出线段DC、DO,写出点D坐标,利用点A、D求出直线AM解析式,与二次函数联立方程组即可求出点M的坐标;
(3)由PR∥AM交AC、BC于R、Q,设出直线PR解析式,分别于二次函数、直线BC联系方程组,即可表示点P、Q坐标,由PQ的长度即可求出点P坐标.
解答 解(1)抛物线y=a(x+1)(x-3),令y=0,
∴x=-1,或x=3,
∴A(-1,0),B(3,0),
∵∠ABC=45°,∠BOC=90°,
∴OB=OC=3,
∴C(0,3),
将点C(0,3)代入二次函数解析式得:
a=-1.
(2)设AM交y轴于点D,作DE⊥AC交AC于点E,如下图:
OA=1,OC=3,
∴AC=$\sqrt{10}$,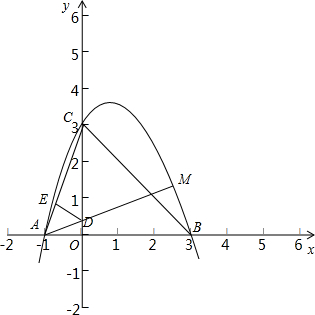
设DE=x,
∵∠CAM=45°,
∴AE=DE=x,CE=10-x,
∵∠DEC=∠AOC,∠ECD=∠OCA,
∴△AOC∽△DEC,
∴$\frac{OA}{ED}$=$\frac{OC}{CE}$,即:$\frac{1}{x}$=$\frac{3}{\sqrt{10}-x}$,
解得:x=$\frac{\sqrt{10}}{4}$,
∴CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=$\sqrt{({\frac{\sqrt{10}}{4})}^{2}+(\sqrt{10}-\frac{\sqrt{10}}{4})^{2}}$=$\frac{5}{2}$,
∴OD=3-$\frac{5}{2}$=$\frac{1}{2}$,
∴D(0,$\frac{1}{2}$),
设直线AM解析式为y=kx+b,(k≠0),将点D(0,$\frac{1}{2}$)、A(-1,0)代入得:
$\left\{\begin{array}{l}{\frac{1}{2}=b}\\{-k+b=0}\end{array}\right.$,解得:k=$\frac{1}{2}$,b=$\frac{1}{2}$,
∴直线AM解析式为y=$\frac{1}{2}$x+$\frac{1}{2}$.
联立:$\left\{\begin{array}{l}{y=\frac{1}{2}x+\frac{1}{2}}\\{y=-(x+1)(x-3)}\end{array}\right.$
解得:x=-1,或x=$\frac{5}{2}$,
将x=$\frac{5}{2}$代入抛物线解析式得:y=$\frac{7}{4}$,
∴M($\frac{5}{2}$,$\frac{7}{4}$).
所以M点横坐标为M($\frac{5}{2}$,$\frac{7}{4}$).
(3)∵PR∥AM,直线AM解析式为y=$\frac{1}{2}$x+$\frac{1}{2}$,
∴设直线PR:y=$\frac{1}{2}$x+b,
联立:$\left\{\begin{array}{l}{y=\frac{1}{2}x+b}\\{y=-x+3}\end{array}\right.$
解得:x=$\frac{6-2b}{3}$,y=$\frac{2b+3}{3}$,
∴Q($\frac{6-2b}{3}$,$\frac{2b+3}{3}$),
联立:$\left\{\begin{array}{l}{y=\frac{1}{2}x+b}\\{y=-(x+1)(x-3)}\end{array}\right.$,
解得:x=$\frac{3±\sqrt{57-16b}}{4}$,
∵点P在第一象限,
∴x=$\frac{3+\sqrt{57-16b}}{4}$
∴y=$\frac{3+8b+\sqrt{57-16b}}{8}$
∴P($\frac{3+\sqrt{57-16b}}{4}$,$\frac{3+8b+\sqrt{57-16b}}{8}$),
∵PQ=$\frac{5}{9}\sqrt{5}$,点P在第一象限,
∴b=$\frac{77+11\sqrt{21}}{36}$,代入点P,
∴P($\frac{\sqrt{21}-1}{6}$,$\frac{19-\sqrt{21}}{6}$).
所以P点横坐标为P($\frac{\sqrt{21}-1}{6}$,$\frac{19-\sqrt{21}}{6}$).
点评 题目考查二次函数综合应用,考查了一次函数解析式求解、二次函数解析式求解、相似三角形、两点间距离等知识点,题目包含知识点较多,对学生的能力要求较高,对学生备战中考压轴训练有很大的提高作用.


科目:初中数学 来源: 题型:选择题
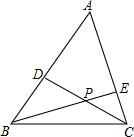 如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=85°,则∠DPE=( )
如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=85°,则∠DPE=( )| A. | 100° | B. | 130° | C. | 120° | D. | 95° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
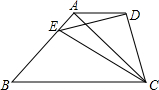 如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,点E是边AB上的一点,∠ECD=45°,那么下列结论错误的是( )
如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,点E是边AB上的一点,∠ECD=45°,那么下列结论错误的是( )| A. | ∠AED=∠ECB | B. | ∠ADE=∠ACE | C. | BE=$\sqrt{2}$AD | D. | BC=$\sqrt{2}$CE |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
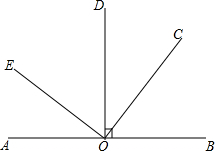 如图,直线AB上有一点O,∠DOB=90°,另有一顶点在O点的直∠EOC.
如图,直线AB上有一点O,∠DOB=90°,另有一顶点在O点的直∠EOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点P、Q在函数y=$\frac{12}{x}$(x>0)的图象上,PA、QB分别垂直x轴于点A、B,PC、QD分别垂直y轴于点C、D.设点P的横坐标为m,点Q的纵坐标为n,△PCD的面积为S1,△QAB的面积为S2.
如图,在平面直角坐标系中,点P、Q在函数y=$\frac{12}{x}$(x>0)的图象上,PA、QB分别垂直x轴于点A、B,PC、QD分别垂直y轴于点C、D.设点P的横坐标为m,点Q的纵坐标为n,△PCD的面积为S1,△QAB的面积为S2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,-4) | B. | (4,-3) | C. | (-4,-3) | D. | (-4,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com