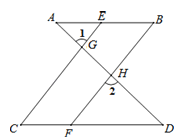
【题目】如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．理由如下：
∵∠1=∠2（已知），
且∠1=∠CGD（___ ___）
∴∠2=∠CGD（等量代换）
∴CE∥BF（__ ___）
∴∠____ ____=∠BFD（___ ____）
又∵∠B=∠C（已知）
∴____ ____（等量代换）
∴AB∥CD（___ ____）
【答案】对顶角相等；同位角相等，两直线平行；C；两直线平行，同位角相等；∠BFD=∠B；内错角相等，两直线平行
【解析】根据对顶角性质和已知推出∠2=∠CGD，推出CE∥BF，根据平行线的性质推出∠BFD=∠B即可；
解：如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．理由如下：
∵∠1=∠2（已知），
且∠1=∠CGD（对顶角相等）
∴∠2=∠CGD（等量代换）
∴CE∥BF（同位角相等，两直线平行）
∴∠C=∠BFD（两直线平行，同位角相等）
又∵∠B=∠C（已知）
∴∠BFD=∠B（等量代换）
∴AB∥CD（内错角相等，两直线平行）
“点睛”本题考查了平行线的性质和判定的应用，主要检查学生能否熟练地运用平行线的性质和判定进行推理和证明，题目比较典型．
云南师大附小一线名师提优作业系列答案科目：初中数学 来源： 题型：
【题目】如图，已知：△ABC内接于⊙O，点D在OC的延长线上，sinB=
，∠D=30度．
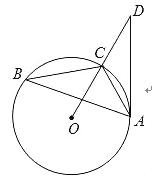
（1）求证：AD是⊙O的切线；
（2）若AC=6，求AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是抛物线y1＝ax2＋bx＋c(a≠0)图象的一部分，抛物线的顶点坐标A(1，3)，与x轴的一个交点B(4，0)，直线y2＝mx＋n(m≠0)与抛物线交于A，B两点，下列结论：
①2a＋b＝0；
②abc>0；
③方程ax2＋bx＋c＝3有两个相等的实数根；
④抛物线与x轴的另一个交点是(－1，0)；
⑤当1<x<4时，有y2<y1，
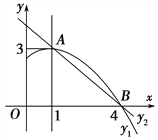
其中正确的是（ ）．
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列推理过程，在括号中填写理由．
如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D．试说明：AC∥DF．
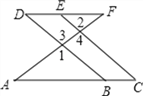
解：∵∠1=∠2（已知），∠1=∠3（______________），
∴∠2=∠3（___________________）．
∴__∥__（__________________________________）．
∴∠C=∠ABD （________________________________）．
又∵∠C=∠D（____________），
∴∠D=∠ABD（等量代换）
∴AC∥DF（______________________________）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形BCDE的各边分别平行于
轴或
轴，物体甲和物体乙由点（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2015次相遇地点的坐标
是（ ）
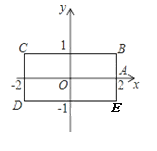
A. （-1，1） B. （1，-1） C. （-2，0） D. （-1，-1）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面几何的学习过程中，我们经常会研究角和线之间的关系．
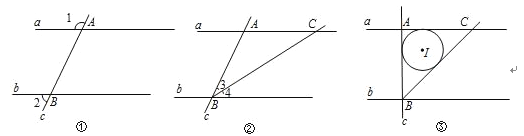
（1）如图①，直线a、b被直线c所截，交点分别为A、B．当∠1、∠2满足数量关系 时，a∥b；
（2）如图②，在（1）中，作射线BC，与直线a的交点为C，当∠3、∠4满足何种数量关系时，AB=AC？证明你的结论；
（3）如图③，在（2）中，若∠BAC=90°，AB=2，⊙I为△ABC的内切圆．
①求⊙I的半径；
②P为直线a上一点，若⊙I上存在两个点M、N，使∠MPN=60°，直接写出AP长度的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，P为正方形ABCD的边BC上一动点（P与B、C不重合），连接AP，过点B作BQ⊥AP交CD于点Q，将△BQC沿BQ所在的直线对折得到△BQC′，延长QC′交BA的延长线于点M．
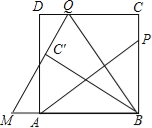
（1）试探究AP与BQ的数量关系，并证明你的结论；
（2）当AB=3，BP=2PC，求QM的长；
（3）当BP=m，PC=n时，求AM的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com