
����Ŀ����ͼ�����κ���y��a��x2+2mx��3m2��������a��m�dz���a��0��m��0����ͼ����x��ֱ���A��B����Aλ�ڵ�B���Ҳࣩ����y�ύ�ڵ�C��0��3������D�ڶ��κ�����ͼ���ϣ�CD��AB������AD������A������AE�����κ�����ͼ���ڵ�E��ABƽ�֡�DAE��
��1����a��m�Ĺ�ϵʽ��
��2����֤��![]() Ϊ��ֵ��
Ϊ��ֵ��
��3����ö��κ�����ͼ��Ķ���ΪF��̽������x������������Ƿ���ڵ�G������GF�����߶�GF��AD��AE�ij���Ϊ���߳�����������ֱ�������Σ�������ڣ�ֻҪ�ҳ�һ������Ҫ��ĵ�G���ɣ����ú�m�Ĵ���ʽ��ʾ�õ�ĺ����ꣻ��������ڣ���˵�����ɣ�
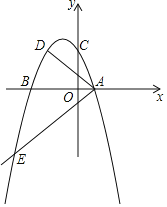
���𰸡���1��am2����1����2��֤������������3�����ڣ���G�ĺ�����Ϊ3m��
��������
��1������C��������������߱���ʽ��������⣻
��2��֤��RtADM����Rt��ANE�������E��x��![]() ��������E��������������߱���ʽ���õ�E����4m����5����������⣻
��������E��������������߱���ʽ���õ�E����4m����5����������⣻
��3�������F����m��4�����õ�ֱ��FC�ı���ʽ�������G��3m��0����������⣮
�⣺��1������C��������������߱���ʽ�ã���3am2��3��
��ã�am2����1��
��2�����ڶ��κ���y��a��x2+2mx��3m2������y��0����x��m��3m��
�ຯ���ĶԳ���Ϊ��x����m��
��CD��AB��
���D��C����������ͬ���ʵ�D����2m��3����
�ʵ�A��B������ֱ�Ϊ����m��0��������3m��0����
���E��x��y����y��a��x2+2mx��3m2����
�ֱ����D��E��x��Ĵ��ߣ�����ֱ�ΪM��N��
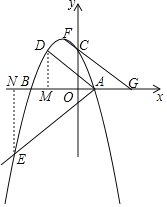
��ABƽ�֡�DAE��
���DAM����EAN��
��RtADM����Rt��ANE��
��![]() ����
����![]() ��
��
��ã�y��![]() ��
��
�ʵ�E��x��![]() ����
����
����E��������������߱���ʽ����ã�x����4m��
��y��![]() ����5��
����5��
�ʵ�E����4m����5����
��![]() ��
��![]() ��
��![]() Ϊ��ֵ��
Ϊ��ֵ��
��3�����ڣ����ɣ�
�����ĶԳ���Ϊx����m����x����mʱ��y��a��x2+2mx��3m2����4������F����m��4����
�ɵ�F��C������ã�ֱ��FC�ı���ʽΪ��y����![]() x+3����y��0����x��3m������G��3m��0����
x+3����y��0����x��3m������G��3m��0����
GF2����3m+m��2+42��16m2+16��
ͬ��AD2��9m2+9��AE2��25m2+25��
��AE2��AD2+GF2��
GF��AD��AE�ij���Ϊ���߳�����������ֱ�������Σ�
��G�ĺ�����Ϊ3m��


 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �У�
��![]() ������
������![]() ��
��
��1����![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��
����ͼ![]() ����
����![]() ���ҵ�
���ҵ�![]() ��
��![]() �е㣬��֤
�е㣬��֤![]() ��
��
����ͼ![]() ����
����![]() ����
����![]() ����֤��
����֤��![]() ��
��
��2����ͼ![]() ����
����![]() ��
��![]() ʱ����
ʱ����![]() ��
��![]() ���ٶȴ�
���ٶȴ�![]() ��
��![]() ����
����![]() ��
��![]() ���ٶȴ�
���ٶȴ�![]() ��
��![]() ������
������![]() ��
��![]() ʱ���㶼ֹͣ�˶������
ʱ���㶼ֹͣ�˶������![]() ���˶�ʱ��
���˶�ʱ��![]() Ϊ����ʱ��
Ϊ����ʱ��![]() �����
�����![]() ��С����С���Ϊ���٣�
��С����С���Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���мס������Ҳ�ݮ��ժ����ݮ�����ۼ۸���䣬���������������Ҿ��ų��Żݷ���.�����Żݷ�����:��ժ�IJ�ݮ������![]() ʱ����ԭ�����ۣ�������
ʱ����ԭ�����ۣ�������![]() ��������
��������![]() ���Żݣ������Żݷ�����:�οͽ��蹺��
���Żݣ������Żݷ�����:�οͽ��蹺��![]() Ԫ��Ʊ.��ժ�IJ�ݮֱ�Ӱ����۳���.��֪�ڼ�������ժ��ݮ
Ԫ��Ʊ.��ժ�IJ�ݮֱ�Ӱ����۳���.��֪�ڼ�������ժ��ݮ![]() ʱ�����������ͬ.
ʱ�����������ͬ.
���Ҳ�ժ�������![]() ( Ԫ)���÷��ժ��
( Ԫ)���÷��ժ��![]() (ǧ��)����һ�κ�����ϵ�����±�:
(ǧ��)����һ�κ�����ϵ�����±�:
���� |
|
|
|
| ������ |
���� |
|
|
|
| ������ |
��1����![]() ��
��![]() �ĺ�����ϵʽ(����д��
�ĺ�����ϵʽ(����д��![]() �ķ�Χ)��
�ķ�Χ)��
��2����������ժ�IJ�ݮ����������ǰ�����ۼ۸�.�����ڼײ�ժ�������![]() (Ԫ)���ݮ��ժ��
(Ԫ)���ݮ��ժ��![]() (ǧ��)�ĺ�����ϵʽ
(ǧ��)�ĺ�����ϵʽ![]() ��
��
��3��������������![]() Ԫȥ��ժ��ݮ��ȥ�ĸ���ժ�����Եõ����������IJ�ݮ�� ˵������.
Ԫȥ��ժ��ݮ��ȥ�ĸ���ժ�����Եõ����������IJ�ݮ�� ˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
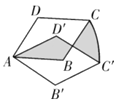
����Ŀ����ͼ����ͼ��������![]() �У�
��![]() ��
��![]() ��������
��������![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת30���õ�����
˳ʱ����ת30���õ�����![]() �����е�
�����е�![]() ���˶�·��Ϊ
���˶�·��Ϊ![]() ����ͼ����Ӱ���ֵ����Ϊ_________��
����ͼ����Ӱ���ֵ����Ϊ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O�İ뾶��3����A��B��C�ڡ�O�ϣ����ı���OABCΪ���Σ���ͼ����Ӱ�������Ϊ_____��
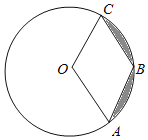
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D����ABC��BC����һ�㣬����AD������ABD�����Բ������ADC��ֱ��AD�۵�����C�Ķ�Ӧ��E���ڡ�O�ϣ�
��1����֤��AE��AB��
��2����գ�
�ٵ���CAB��90����cos��ADB��![]() ��BE��2ʱ����BC�ij�Ϊ�� ����
��BE��2ʱ����BC�ij�Ϊ�� ����
�ڵ���BAE���� ��ʱ���ı���AOED�����Σ�
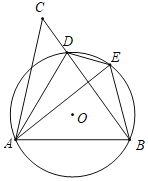
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������С��Ҫ��������һ�����ĸ߶�AB������һ��С���Ավ�ھ�����10�ĵ�E�����������A������Ϊ54��.��֪����ǵļܸ�CE��1.8�ף���������ĸ߶�Ϊ_________��.���������һλС��.�ο����ݣ�sin54�㣽0.8090��cos54�㣽0.5878��tan54�㣽1.3764��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ƻ�����A��B�����ͺŵĻ����˰��˲��ϣ���֪A�ͻ����˱�B�ͻ�����ÿСʱ�����30kg���ϣ���A�ͻ����˰���1000kg�������õ�ʱ����B�ͻ����˰���800kg�������õ�ʱ����ͬ��
��1����A��B�����ͺŵĻ�����ÿСʱ�ֱ���˶��ٲ��ϣ�
��2���ù�˾�ƻ��ɹ�A��B�����ͺŵĻ����˹�20̨��Ҫ��ÿСʱ���˲��ϲ�������2800kg�������ٹ���A�ͻ����˶���̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ̨������ˮƽ�����ϵıʼDZ����ԣ��������������ͼ2��ʾ�ļ���ͼ��.����ʾ��AO�����BO����Ϊ24cm����PΪ�۾�����λ�ã�DΪAO���е㣬����PD����PD��AO����ʱ��PΪ����ӽǣ�����C��OB���ӳ����ϣ�PC��BC��BC��12cm.
��1����PA��45cmʱ����PC�ij���
��2������AOC��115��ʱ���߶�PC�ij��ȣ�1�����߶�PC�ij��������Ǽ�С����ͨ������˵�����������ȷ��0.1cm��sin65���0.91��cos65���0.42��tan65���2.14��sin25���0.42��cos25���0.91��tan25���0.47��.
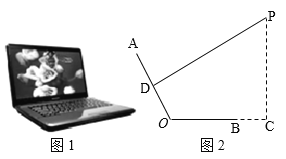
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com