
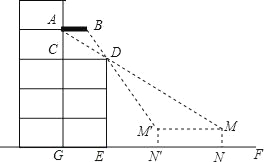
【题目】周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处,这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,MN=M′N′,露台的宽CD=GE.实际测得,GE=5米,EN=15.5米,NN′=6.2米.请根据以上信息,求出遮阳篷的宽AB是多少米?
科目:初中数学 来源: 题型:
【题目】点P(a,b)是直线y=-x-5与双曲线![]() 的一个交点,则以a、b两数为根的一元二次方程是( ).
的一个交点,则以a、b两数为根的一元二次方程是( ).
A. x2-5x+6=0 B. x2+5x+6=0 C. x2-5x-6="0" D. x2+5x-6=0
查看答案和解析>>
科目:初中数学 来源: 题型:
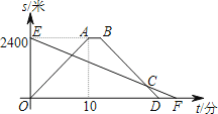
【题目】一条笔直的公路上有甲乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地.设他们同时出发,运动的时间为t(分),与乙地的距离为s(米),图中线段EF,折线OABD分别表示两人与乙地距离s和运动时间t之间的函数关系图象.
(1)李越骑车的速度为______米/分钟;
(2)B点的坐标为______;
(3)李越从乙地骑往甲地时,s与t之间的函数表达式为______;
(4)王明和李越二人______先到达乙地,先到______分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以O为位似中心将四边形ABCD放大后得到四边形A'B'C'D',若OA=4,OA'=8,则四边形ABCD和四边形A'B'C'D'的周长的比为( )
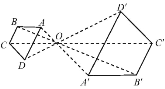
A. 1∶2 B. 1∶4
C. 2∶1 D. 4∶1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为开拓学生的视野,全面培养和提升学生的综合素质,让学生感受粤东古城潮州的悠久历史,某中学组织八年级师生共420人前往潮州开展研学活动.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车5辆,则空余15个座位;若租用A型车5辆,B型车3辆,则15人没座位.
(1)求A、B两种车型各有多少个座位?
(2)租车公司目前B型车只有6辆,若A型车租金为1800元/辆,B型车租金为2100元/辆,请你为学校设计使座位恰好坐满师生且租金最少的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,新农村改造过程中需要修建污水处理厂,如图,![]() 、
、![]() 是位于直线小河
是位于直线小河![]() 同侧的两个村庄,
同侧的两个村庄,![]() 村距离小河
村距离小河![]() 的距离
的距离![]() ,
,![]() 村距离小河
村距离小河![]() 的距离
的距离![]() ,经测量
,经测量![]() ,现准备在小河边修建一个污水处理厂
,现准备在小河边修建一个污水处理厂![]() .(不考虑河宽)
.(不考虑河宽)
(1)设![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的长(保留根号);
的长(保留根号);
(2)为了节省材料,使得两村的排污管道最短,求最短的排污管长;
(3)根据(1)(2)的结果,运用数形结合思想,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
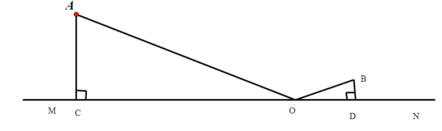
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E. F,分别以E. F为圆心,以大于![]() EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )
EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是( )

A.∠ADB=∠ABCB.AB=BDC.AC=AD+BDD.∠ABD=∠BCD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com