
【题目】为了保护环境,新农村改造过程中需要修建污水处理厂,如图,![]() 、
、![]() 是位于直线小河
是位于直线小河![]() 同侧的两个村庄,
同侧的两个村庄,![]() 村距离小河
村距离小河![]() 的距离
的距离![]() ,
,![]() 村距离小河
村距离小河![]() 的距离
的距离![]() ,经测量
,经测量![]() ,现准备在小河边修建一个污水处理厂
,现准备在小河边修建一个污水处理厂![]() .(不考虑河宽)
.(不考虑河宽)
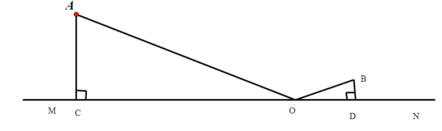
(1)设![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的长(保留根号);
的长(保留根号);
(2)为了节省材料,使得两村的排污管道最短,求最短的排污管长;
(3)根据(1)(2)的结果,运用数形结合思想,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)25米;(3)17
;(2)25米;(3)17
【解析】
(1)根据勾股定理即可得到结论;
(2)作点A关于直线MN的对称点A′,连接A′B交MN于O,此时,OA+OB=OB+OA′的长最短,即点O即为污水处理厂的位置,根据勾股定理即可得到结论;
(3)由(2)可知,作出图形,利用最短路径问题和勾股定理解题,即可得到答案.
解:(1)在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
∴![]() .
.
(2)作点![]() 关于
关于![]() 对称点为
对称点为![]() ,可以得到,
,可以得到,![]() .
.
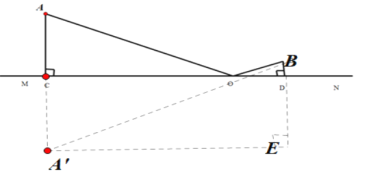
根据两点之间线段最短可以得到,![]() 的长度就是最短的排污管.
的长度就是最短的排污管.
∵![]() ,
,![]() ,
,
由勾股定理得:![]() .
.
(3)根据(2)的结果,先作对称点,把问题转化到求最短距离问题.如图:
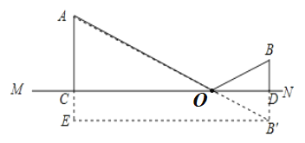
设BD=2,AC=6,CD=15,设OC=a,则OD=15-a,
根据勾股定理得,AO+OB=![]() ,
,
此时![]() ,
,
当A、O、B′三点共线时,OA+OB的值最小,
∴![]() 的值最小,即
的值最小,即![]() 的长度;
的长度;
∴最小值为:![]() ;
;
∴![]() 的最小值为17.
的最小值为17.


科目:初中数学 来源: 题型:
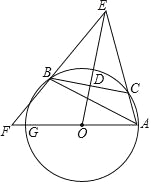
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
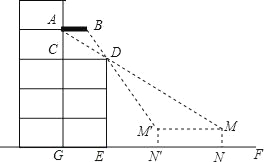
【题目】周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处,这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,MN=M′N′,露台的宽CD=GE.实际测得,GE=5米,EN=15.5米,NN′=6.2米.请根据以上信息,求出遮阳篷的宽AB是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.
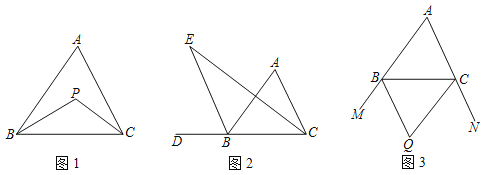
(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC= ;
(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);
(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC与∠A的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
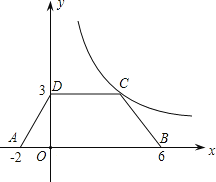
【题目】如图,等腰梯形ABCD放置在平面坐标系中,已知A(﹣2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
(1)求点C的坐标和反比例函数的解析式;
(2)将等腰梯形ABCD向上平移2个单位后,问点B是否落在双曲线上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在直角![]() 中,
中,![]() ,点
,点![]() 是
是![]() 中点,连接
中点,连接![]() ,点
,点![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 交线段
交线段![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
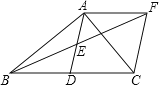
(1)求证:![]() ;
;
(2)在不添加任何辅助线的情况下,请直接写出所有面积等于![]() 面积
面积![]() 倍的三角形.
倍的三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com