练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

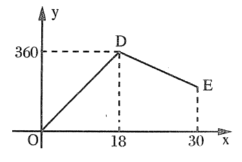
    【题目】某公司开发一种新的节能产品，工作人员对销售情况进行了调查，图中折线表示月销售量(件)与销售时间(天)之间的函数关系，已知线段表示函数关系中，时间每增加天，月销售量减少件，求与间的函数表达式．

    【答案】．

    【解析】

    由时间每增加1天日销售量减少5件结合第18天的日销售量为360件，即可求出第19天的日销售量，再根据点的坐标，利用待定系数法可求出直线OD、DE的函数关系式，即可找出y与x之间的函数关系式；

    当时，

    设直线OD的解析式为

    将代入得，

    ∴，

    ∴直线OD的解析式为：，

    当时，

    根据题意“时间每增加天，月销售量减少件”，则第19天的日销售量为：360-5=355，

    设直线DE的解析式为，

    将，代入得，

    解得：，

    ∴直线DE的解析式为，

    ∴与间的函数表达式为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠BAC＝60°，D是AB上一点，AC＝BD，P是CD中点．求证：AP＝BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

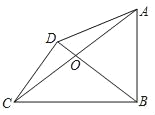
    【题目】如图，在四边形ABCD中，∠ABC＝90°，对角线AC、BD交于点O，AO＝CO，CD⊥BD，如果CD＝3，BC＝5，那么AB＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，如果某点的横坐标与纵坐标的和为10，则称此点为“合适点”例如，点（1，9），（﹣2019，2029）…都是“合适点”．

    （1）求函数y＝2x+1的图象上的“合适点”的坐标；

    （2）求二次函数y＝x2﹣5x﹣2的图象上的两个“合适点”A，B之间线段的长；

    （3）若二次函数y＝ax2+4x+c的图象上有且只有一个合适点”，其坐标为（4，6），求二次函数y＝ax2+4x+c的表达式；

    （4）我们将抛物线y＝2（x﹣n）2﹣3在x轴下方的图象记为G1，在x轴及x轴上方图象记为G2，现将G1沿x轴向上翻折得到G3，图象G2和图象G3两部分组成的记为G，当图象G上恰有两个“合适点”时，直接写出n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

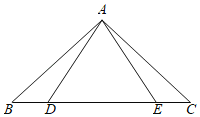
    【题目】如图，在△ABC中，∠B＝∠C＝44°，点D点E分别从点B、点C同时出发，在线段BC上作等速运动，到达C点、B点后运动停止．

    （1）求证：△ABE≌△ACD；

    （2）若AB＝BE，求∠DAE的度数；

    （3）若△ACE的外心在其内部时，求∠BDA的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

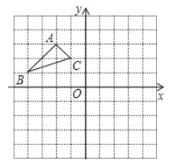
    【题目】如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A(-2，3)，B(-4，1)，C(-1，2)．

    （1）画出以点O为旋转中心，将△ABC顺时针旋转90°得到△A'B'C'

    （2）求点C在旋转过程中所经过的路径的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A，B，C，D在⊙O上，AB=AC，∠A=40°，CD∥AB，若⊙O的半径为2，则图中阴影部分的面积是(　　)

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：同时经过x轴上两点A，B（m≠n）的两条抛物线称为同弦抛物线．如抛物线C1：与抛物线C2：是都经过，的同弦抛物线．

    （1）引进一个字母，表达出抛物线C1的所有同弦抛物线；

    （2）判断抛物线C3：与抛物线C1是否为同弦抛物线，并说明理由；

    （3）已知抛物线C4是C1的同弦抛物线，且过点，求抛物线C对应函数的最大值或最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为营造“安全出行”的良好交通氛围,实时监控道路交迸,某市交管部门在路口安装的高清摄像头如图所示,立杆MA与地面AB垂直,斜拉杆CD与AM交于点C,横杆DE∥AB,摄像头EF⊥DE于点E,AC=55米,CD=3米,EF=0.4米,∠CDE=162°。

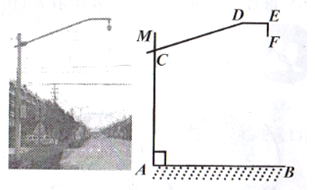
    （1）求∠MCD的度数；

    （2）求摄像头下端点F到地面AB的距离。(精确到百分位)

    （参考数据;sin72°=0.95，cos72°≈0.31,tan72°=3.08,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32）

    查看答案和解析>>

    同步练习册答案