
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.


【考点】平行四边形的判定;菱形的判定.
【分析】(1)由AE=DF,∠A=∠D,AB=DC,易证得△AEC≌△DFB,即可得BF=EC,∠ACE=∠DBF,且EC∥BF,即可判定四边形BFCE是平行四边形;
(2)当四边形BFCE是菱形时,BE=CE,根据菱形的性质即可得到结果.
【解答】(1)证明:∵AB=DC,
∴AC=DB,
在△AEC和△DFB中
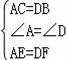
 ,
,
∴△AEC≌△DFB(SAS),
∴BF=EC,∠ACE=∠DBF
∴EC∥BF,
∴四边形BFCE是平行四边形;
(2)当四边形BFCE是菱形时,BE=CE,
∵AD=10,DC=3,AB=CD=3,
∴BC=10﹣3﹣3=4,
∵∠EBD=60°,
∴BE=BC=4,
∴当BE=4 时,四边形BFCE是菱形,
故答案为:4.


科目:初中数学 来源: 题型:
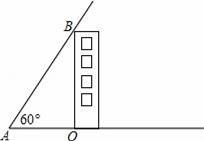
如图,为测量一幢大楼的高度,在地面上距离楼底O点20m的点A处,测得楼顶B点的仰角∠OAB=60°,则这幢大楼的高度为 (用科学计算器计算,结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
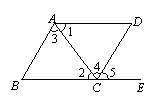
如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为 ……………………………………………………………… ( )
A.①②③④ B.①②④ C.①③④ D.①②③
 | |||
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点A在直线y=x上,AB⊥x轴于点B,点C在线段AB上,以AC为边作正方形ACDE,点D恰好在反比例函数y=
 (k为常数,k≠0)第一象限的图象上,连接AD.若OA2﹣AD2=20,则k的值为 .
(k为常数,k≠0)第一象限的图象上,连接AD.若OA2﹣AD2=20,则k的值为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.
①求证:△BCE是等边三角形;
②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.


查看答案和解析>>
科目:初中数学 来源: 题型:
2016年扬州体育中考现场考试内容有两项,50米跑为必考项目,另在立定跳远、坐位体前屈、实心球和一分钟跳绳中选一项测试.王老师对参加体育中考的九(1)班40名学生的一项选测科目作了统计,列出如图所示的统计表,则本班参加坐位体前屈的人数是 人.
| 组别 | 立定跳远 | 坐位体前屈 | 实心球 | 一分钟跳绳 |
| 频率 | 0.4 | 0.35 | 0.1 | 0.15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com