
如图,点A在直线y=x上,AB⊥x轴于点B,点C在线段AB上,以AC为边作正方形ACDE,点D恰好在反比例函数y=
 (k为常数,k≠0)第一象限的图象上,连接AD.若OA2﹣AD2=20,则k的值为 .
(k为常数,k≠0)第一象限的图象上,连接AD.若OA2﹣AD2=20,则k的值为 .


10 .
【考点】反比例函数与一次函数的交点问题.
【分析】设正方形的边长为a,A(t,t),则OB=AB=t,AC=CD=a,于是可表示出C(t,t﹣a),D(t+a,t﹣a),利用等腰直角三角形的性质得OA=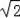
 t,AD=
t,AD=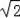
 a,则由OA2﹣AD2=20可得t2﹣a2=10,然后根据反比例函数图象上点的坐标特征得k=(t+a)(t﹣a)=t2﹣a2=10.
a,则由OA2﹣AD2=20可得t2﹣a2=10,然后根据反比例函数图象上点的坐标特征得k=(t+a)(t﹣a)=t2﹣a2=10.
【解答】解:设正方形的边长为a,A(t,t),则OB=AB=t,AC=CD=a,
∴C(t,t﹣a),D(t+a,t﹣a),
∴OA=
 t,AD=
t,AD=
 a,
a,
∵OA2﹣AD2=20,
∴(
 t)2﹣(
t)2﹣(
 a)2=20,
a)2=20,
∴t2﹣a2=10,
∵点D在反比例函数y=
 的图象上,
的图象上,
∴k=(t+a)(t﹣a)=t2﹣a2=10.
故答案为10.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
(1)如图,△ABC中,∠ABC的角平分线与∠ACB的外角 ∠ACD的平分线交于A1. 当∠A为80°时,求∠A1的度数
∠ACD的平分线交于A1. 当∠A为80°时,求∠A1的度数
(2)在上一题中,若∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,则∠A6= .
(3)如图,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F=
(4)如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q —∠A1的值为定值.其中有且只有一个是正确的,请写出正确的结论 (填编号),并写出其值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )


A.6 B.12 C.20 D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
某玩具店进了一箱黑白两种颜色的塑料球3000个(除颜色外都相同),为了估计两种颜色的球各有多少个,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子里,多次重复上述过程后,发现摸到黑球的频率在0.6附近波动,据此可以估算黑球的个数约为 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com