
 如图,在四边形ABCD中,AD=BC,E、F分别是DC及AB的中点,射线FE与AD及BC的延长线分别交于点H及G.试猜想∠AHF与∠BGF的关系,并给出证明.
如图,在四边形ABCD中,AD=BC,E、F分别是DC及AB的中点,射线FE与AD及BC的延长线分别交于点H及G.试猜想∠AHF与∠BGF的关系,并给出证明.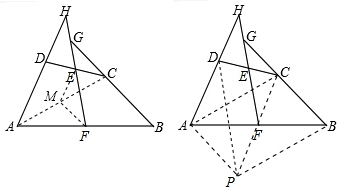 答:∠AHF=∠BGF.
答:∠AHF=∠BGF.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
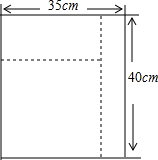 如图所示,有一块长为40cm、宽为35cm的长方形红布,晶晶的妈妈想把它剪成一个正方形,第一次她剪去了一个一定宽度的长方形布片,然后在剩下的长方形布片中又剪去长方形的布片,这次剪去的布片的宽度是上次的2倍,这样剩下的布片恰好是一个正方形,请问晶晶妈妈第一次剪去的长方形布片的宽为多少厘米?
如图所示,有一块长为40cm、宽为35cm的长方形红布,晶晶的妈妈想把它剪成一个正方形,第一次她剪去了一个一定宽度的长方形布片,然后在剩下的长方形布片中又剪去长方形的布片,这次剪去的布片的宽度是上次的2倍,这样剩下的布片恰好是一个正方形,请问晶晶妈妈第一次剪去的长方形布片的宽为多少厘米?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com