【题目】如图所示，ABCD是一个正方形，其中几块阴影部分的面积如图所示，则四边形BMQN的面积为 ．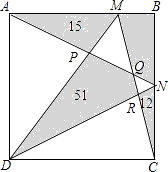 
【答案】24
【解析】解：S四边形BMQN=S正方形ABCD﹣（S△ADN+S△DMC﹣S四边形PQRD）﹣S△APM﹣S△CNR
=S正方形ABCD﹣S正方形ABCD+S四边形PQRD﹣S△APM﹣S△CNR
=51﹣15﹣12
=24．
所以答案是：24．
【考点精析】根据题目的已知条件，利用正方形的性质的相关知识可以得到问题的答案，需要掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
科目：初中数学 来源： 题型：
【题目】为加强爱国主义教育，提高思想道德素质，某中学决定组织部分班级去山西国民师范旧址革命活动纪念馆开展红色旅游活动，在参加此次活动的师生中，若每位教师带17名学生，还剩12名学生没人带；若每位教师带18名学生，就有一位教师少带4名学生．现有甲、乙两种大客车，两种客车的载客量和租金如下表所示．
类别 | 甲种客车 | 乙种客车 |
载客量（人/辆） | 30 | 42 |
租金（元/辆） | 300 | 420 |
（1）参加此次红色旅游活动的教师和学生各有多少人？
（2）为了安全，每辆客车上要有2名教师．则怎样租车可以保证师生均有车坐，而且每辆车上都没有空座，也不超载，此时租车的费用为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等腰Rt△ABC中，∠ACB=90o,AC=CB，F是AB边上的中点,点D、E分别在AC、BC边上运动，且始终保持AD=CE，连接DE、DF、EF．
（1）求证：△ADF≌△CEF；
（2）试证明△DFE是等腰直角三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了调查某小区居民的用水情况，随机抽查了10户家庭的月用水量，结果如下表：
月用水量（吨） | 4 | 5 | 6 | 9 |
户数 | 3 | 4 | 2 | 1 |
则关于这10户家庭的月用水量，下列说法错误的是 （ ）
A.中位数是5吨
B.众数是5吨
C.极差是3吨
D.平均数是5．3吨
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是平行四边形，顶点A、B的坐标分别是A（1，0），B（0，﹣2），顶点C、D在双曲线 
上，边AD与y轴相交于点E， 
=10，则k的值是（ ）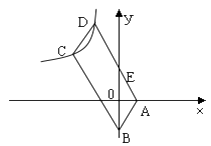
A.-16
B.-9
C.-8
D.-12
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知∠ACB＝90°，AC＝2，CB＝4．点P为线段CB上一动点，连接AP，△APC与△APC′关于直线AP对称，其中点C的对称点为点C′．直线m过点A且平行于CB
（1）如图①：连接AB，当点C落在线段AB上时，求BC′的长；
（2）如图②：当PC＝
BC时，延长PC′交直线m于点D，求△ADC′面积；
（3）在（2）的条件下，连接BC′，直接写出线段BC′的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．
(1)在给定方格纸中画出平移后的△A′B′C′；
(2)画出AB边上的中线CD和BC边上的高线AE；
(3)线段AA′与线段BB′的关系是： ；
(4) 求四边形ACBB′的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC在平面直角坐标系中的位置如图所示．A（2，3），B（3，1），C（﹣2，﹣2）三点在格点上．
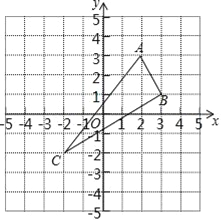
（1）作出△ABC关于y轴对称的△A1B1C1；
（2）直接写出△ABC关于x轴对称的△A2B2C2的各点坐标；
（3）求出△ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
