
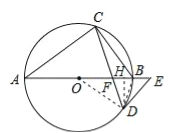
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC

(1)求证:DE与⊙O相切;
(2)若BF=2,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)详见解析;(2)5.
【解析】试题分析:(1)连接OD,由AB是⊙O的直径可得∠ACB=90°,所以∠A+∠ABC=90°,即可证得∠BOD=∠A,从而推出∠ODE=90°,即可得到结论;(2)连接BD,过D作DH⊥BF于H,由弦切角定理得到∠BDE=∠BCD,推出△ACF与△FDB都是等腰三角形,根据等腰直角三角形的性质得到FH=BH=![]() BF=1,则FH=1,根据勾股定理得到HD=3,然后根据勾股定理列方程即可得到结论.
BF=1,则FH=1,根据勾股定理得到HD=3,然后根据勾股定理列方程即可得到结论.
试题解析:(1)证明:连接OD,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
∵∠BOD=2∠BCD,∠A=2∠BCD,
∴∠BOD=∠A,
∵∠AED=∠ABC,
∴∠BOD+∠AED=90°,
∴∠ODE=90°,
即OD⊥DE,
∴DE与⊙O相切;
(2)解:连接BD,过D作DH⊥BF于H,
∵DE与⊙O相切,
∴∠BDE=∠BCD,
∵∠AED=∠ABC,
∴∠AFC=∠DBF,
∵∠AFC=∠DFB,
∴△ACF与△FDB都是等腰三角形,
∴FH=BH=![]() BF=1,则FH=1,由勾股定理可得HD==3,
BF=1,则FH=1,由勾股定理可得HD==3,
在Rt△ODH中,OH2+DH2=OD2,
即(OD﹣1)2+32=OD2,
∴OD=5,
∴⊙O的半径是5.


科目:初中数学 来源: 题型:
【题目】深高北校区初二年级举行“名著知识竟赛”决赛.在这之前,初二(24)班举行了三轮初赛,为了从甲乙两名平均分最高的同学中选取一名发挥稳定的同学参加决赛,需要考察这两位同学三轮初赛成绩的( )
A. 平均数 B. 众数 C. 中位数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
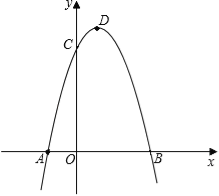
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的三角形纸片中,AB=8cm,BC=6cm,AC=7cm,沿过点B的直线折叠三角形,使点C落在AB边的点E处,折痕为BD,则△AED的周长为 . 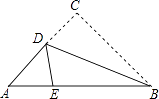
查看答案和解析>>
科目:初中数学 来源: 题型:
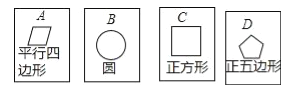
【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市辖区内长江流域水质情况的调查
B.对乘坐飞机的旅客是否携带违禁物品的调查
C.对一个社区每天丢弃塑料袋数量的调查
D.对重庆电视台“天天630”栏目收视率的调查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com