
【题目】已知y+2与x-1成正比例,且x=3时,y=4.
(1)求y与x之间的函数关系式.
(2)求当y=1时x的值.
【答案】
(1)解:设y+2=k(x-1),(k![]() 0)
0)
把x=3时,y=4代入得:4+2=k(3-1),
解得:k=3,
∴y与x之间的函数关系式是:y+2=3(x-1),
即:y=3x-5.
答:y与x之间的函数关系式是:y=3x-5.
(2)解:当y=1时,3x-5=1,
解得:x=2.
答:当y=1时,x=2.
【解析】(1)已知已知y+2与x-1成正比例,即可以设y+2=k(x-1),把x=3时,y=4代入即可求得k的值,进而求出函数解析式;(2)在第(1)问基础上,把y=1代入解析式即可求得x的值.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


科目:初中数学 来源: 题型:
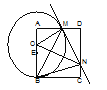
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC

(1)求证:DE与⊙O相切;
(2)若BF=2,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是边AB上一点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连结OM、ON、BM、BN.
求证:(1)△AOM∽△DMN; (2)求∠MBN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习完一次函数后,小荣遇到过这样的一个新颖的函数:y=|x﹣1|,小荣根据学校函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小荣的探究过程,请补充完成: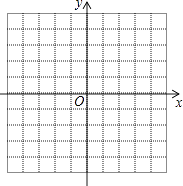
(1)列表:下表是y与x的几组对应值,请补充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 4 | 2 | 1 | … |
(2)描点连线:在平面直角坐标系xOy中,请描出以上表中各对对应值为坐标的点,画出该函数的图象;
(3)进一步探究发现,该函数图象的最低点的坐标是(1,0),结合函数的图象,写出该函数的其他性质(一条即可): .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一粒芝麻约有0.000002千克,0.000002用科学记数学法表示为( )千克.
A.2×10﹣4
B.0.2×10﹣5
C.2×10﹣7
D.2×10﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
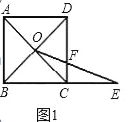
【题目】数学课上,张老师出示了问题1:如图1,四边形ABCD是正方形,BC=1,对角线交点记作O,点E是边BC延长线上一点.连接OE交CD边于F,设CE=x,CF=y,求y关于x的函数解析式及其定义域.
(1)经过思考,小明认为可以通过添加辅助线﹣﹣过点O作OM⊥BC,垂足为M求解.你认为这个想法可行吗?请写出问题1的答案及相应的推导过程;
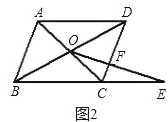
(2)如果将问题1中的条件“四边形ABCD是正方形,BC=1”改为“四边形ABCD是平行四边形,BC=3,CD=2,”其余条件不变(如图2),请直接写出条件改变后的函数解析式;
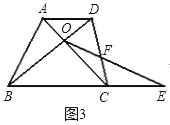
(3)如果将问题1中的条件“四边形ABCD是正方形,BC=1”进一步改为:“四边形ABCD是梯形,AD∥BC,BC=a,CD=b,AD=c(其中a,b,c为常量)”其余条件不变(如图3),请你写出条件再次改变后y关于x的函数解析式以及相应的推导过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com