
【题目】如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
(1)试猜想DE与BF的关系,并证明你的结论;
(2)求证:MB=MD.
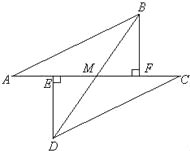
【答案】(1)证明见解析 (2)证明见解析
【解析】
试题(1)根据BF⊥AC,DE⊥AC,AE=CF AF=AE+EF CE=CF+EF,可以证明Rt△ABF≌Rt△CDE,得DE=
BF;再根据BF⊥AC,DE⊥AC,可以证明DE//BF.(2)根据(1)中的结论,可证△BFM≌△DEM,从而证明MB=MD.
试题解析:(1)①DE与BF的关系可以有DE=BF成立,理由如下:
∵AE=CF AF=AE+EF CE=CF+EF
∴AF=CE 又∵BF⊥AC,DE⊥AC
∴∠BFA=∠DEC=90°
在Rt△ABF和Rt△CDE中
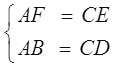
∴Rt△ABF≌Rt△CDE (HL)
∴DE=BF(全等三角形对应边相等)
②DE与BF的关系可以有DE//BF,理由如下:
∵DE⊥AC BF⊥AC
∴DE//BF
(2)证明:
∵Rt△ABF≌Rt△CDE
∴BF=ED
在△BFM和△DEM中
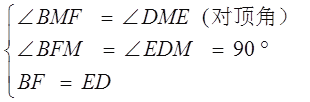
∴△BFM≌△DEM (AAS)
∴MB=MD


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)写出数轴上点A表示的数;
(2)将长方形OABC沿数轴向右水平移动,移动后的长方形记为![]() ,若移动后的长方形
,若移动后的长方形![]() 与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的
与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的![]() 时,写出数轴上点
时,写出数轴上点![]() 表示的数;
表示的数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡顶A处的俯角为15°,山脚处B的俯角为60°,已知该山坡的坡度i=1: ![]() ,点P、H,B,C,A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为( )
,点P、H,B,C,A在同一个平面上,点HBC在同一条直线上,且PH⊥BC,则A到BC的距离为( )
A.10 ![]() 米
米
B.15米
C.20 ![]() 米
米
D.30米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形ABCD中,F是CD边上一点(不和C,D重合),过点D做DG⊥BF交BF延长线于点G.连接AG,交BD于点E,连接EF,交CD于点M.若DG=6,AG=7 ![]() ,则EF的长为 .
,则EF的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.

(1,1),(3,1),(1,3),(1,1);
(-1,3),(-1,5),(-3,3),(-1,3);
(-5,1),(-3,-1),(-3,1),(-5,1);
(-1,-1),(1,-1),(-1,-3),(-1,-1).
(1)观察所得的图形,你觉得它像什么?
(2)求出这四个图形的面积和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,
,![]() ,
,![]() ,把
,把![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转一周,同时
的速度逆时针方向旋转一周,同时![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转,当
的速度逆时针方向旋转,当![]() 停止旋转时
停止旋转时![]() 也随之停止旋转.设旋转后的两个角分别记为
也随之停止旋转.设旋转后的两个角分别记为![]() 、
、![]() ,旋转时间为
,旋转时间为![]() 秒.
秒.
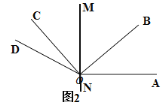
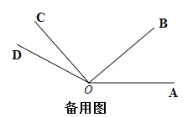
(1)如图2,直线![]() 垂直于
垂直于![]() ,将
,将![]() 沿直线
沿直线![]() 翻折至
翻折至![]() ,请你直接写出
,请你直接写出![]() 的度数,不必说明理由;
的度数,不必说明理由;
(2)如图1,在旋转过程中,若射线![]() 与
与![]() 重合时,求
重合时,求![]() 的值;
的值;
(3)如图1,在旋转过程中,当![]() 时,直接写出
时,直接写出![]() 的值,不必说明理由.
的值,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,在四边形 ABCD 中,AB∥DC,E 是 BC 中点,若 AE 是∠BAD 的平分线,试探究 AB,AD,DC 之间的数量关系,请直接写出结论,无需证明.
(2)如图 2,在四边形ABCD 中,AB∥DC,AF 与DC 的延长线交于点F,E 是BC 中点,若AE 是∠BAF 的平分线,试探究AB,AF,CF 之间的数量关系,证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AD=8cm,AB=6cm,动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动,E点运动到B点停止,F点继续运动,运动到点D停止.如图可得到矩形CFHE,设F点运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是如图中的( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com