
【题目】某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表:
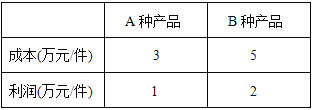
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)条件下,哪种方案获利最大?并求最大利润.
【答案】(1)A产品生产6件,B产品生产4件.(2)所以方案一:A生产3件B生产7件;方案二:A生产4件,B生产6件;方案三:A生产5件,B生产5件.(3)第一种方案获利最大,17万元.
【解析】(1)设A种产品x件,B种为(10﹣x)件,根据共获利14万元,列方程求解.
(2)设A种产品x件,B种为(10﹣x)件,根据若工厂投入资金不多于44万元,且获利多于14万元,列不等式组求解.
(3)设A种产品x件,所获利润为y万元,求出利润的表达式,利用一次函数的性质求解即可.
(1)设A种产品x件,B种为(10﹣x)件,x+2(10﹣x)=14,解得:x=6.
答:A生产6件,B生产4件.
(2)设A种产品x件,B种为(10﹣x)件,根据题意得:
![]() ,
,
解得:3≤x<6.
∵x为正整数,∴有三种方案,具体如下:
方案一:A生产3件 B生产7件;
方案二:A生产4件,B生产6件;
方案三:A生产5件,B生产5件.
(3)第一种方案获利最大.
设A种产品x件,所获利润为y万元,∴y=x+2(10﹣x)=﹣x+20.
∵k=﹣1<0,∴y随x的增大而减小,∴当x=3时,获利最大,∴3×1+7×2=17,最大利润是17万元.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线AC、BD相交于点O,延长AB至点E,使BE=AB,连接CE.

(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AC=![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣3,2),B(﹣4,1),C(﹣2,0).

(1)若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;
(2)若△A2B2C2与△ABC是中心对称图形,则对称中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于![]() 轴对称,若△OAB的面积为6,求m的值.
轴对称,若△OAB的面积为6,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=x+b与x轴交于点A(2,0),P为y轴上B点下方一点,以AP为腰作等腰直角三角形APM,点M落在第四象限,若PB=m(m>0),用含m的代数式表示点M的坐标是( )

A.(m-2,m+4)B.(m+2,m+4)C.(m+2,-m-4)D.(m-2,-m-4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=-x2+ax+b的图象与x轴交于A(-![]() ,0),B(2,0)两点,且与y轴交于点C.
,0),B(2,0)两点,且与y轴交于点C.
(1)求该抛物线的解析式,并判断△ABC的形状;
(2)设P是x轴上方的抛物线上的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、A 、M为顶点的三角形与ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(x-m)2-(x-m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=![]() .
.
①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
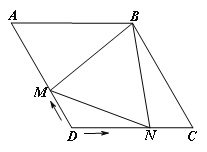
【题目】如图,菱形ABCD,∠A=60°,AB=6,点M从点D向点A以1个单位∕秒的速度运动,同时点N从点D向点C以2个单位∕秒的速度运动,连结BM、BN,当△BMN为等边三角形时,![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某排球队6名上场队员的身高(单位:![]() )是:180,184,188,190,192,194,现用一名身高为
)是:180,184,188,190,192,194,现用一名身高为![]() 的队员换下场上身高为
的队员换下场上身高为![]() 的队员,与换人前相比,场上队员的身高平均数________.填“变大”.“不变”.“变小”),方差________.(填“变大”.“不变”.“变小”)
的队员,与换人前相比,场上队员的身高平均数________.填“变大”.“不变”.“变小”),方差________.(填“变大”.“不变”.“变小”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com