
【题目】已知:如图,直线y=x+b与x轴交于点A(2,0),P为y轴上B点下方一点,以AP为腰作等腰直角三角形APM,点M落在第四象限,若PB=m(m>0),用含m的代数式表示点M的坐标是( )

A.(m-2,m+4)B.(m+2,m+4)C.(m+2,-m-4)D.(m-2,-m-4)
【答案】C
【解析】
先利用待定系数法求出直线AB的函数解析式,从而得OP的长,再证△PAO≌△MPN,得到OP=NM,OA=NP,进而用m表示出NM和ON,结合点M在第四象限,表示出点M的坐标即可.
直线y=x+b与x轴交于点A(2,0),
∴0=2+b,解得:b=-2,
∴直线AB的解析式为:y=x2,
令x=0,得y=-2,
∴B(0,-2),
∵PB=m,
∴OP=2+m,
作MN⊥y轴于点N.
∵△APM为等腰直角三角形,PM=PA,
∴∠APM=90°,
∴∠OPA+∠NPM=90°,
∵∠NMP+∠NPM=90°,
∴∠OPA=∠NMP,
在△PAO与△MPN中,
∵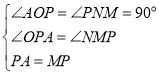 ,
,
∴△PAO≌△MPN(AAS),
∴OP=NM= m+2,OA=NP=2,
∴ON=2+m+2=4+m,MN=OP=2+m,
∵点M在第四象限,
∴点M的坐标为(2+m,4m).
故选C.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
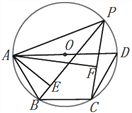
【题目】如图:点P是四边形ABCD外接圆⊙O上的任意一点,且不与四边形顶点重合,若AD是⊙O的直径,AB=BC=CD,连接PA,PB,PC,若PA= ![]() ,求点A到PB和PC的距离之和AE+AF是多少?
,求点A到PB和PC的距离之和AE+AF是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).
的图象与x轴交于A、B两点,与y轴交于C点,已知点B坐标为(4,0).

(1)求抛物线的解析式;
(2)判断△ABC的形状,直接写出△ABC外接圆的圆心坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店出售某种水果,已知该水果的进价为6元/千克,若以9元/千克的价格销售,则每天可售出200千克;若以11元/千克的价格销售,则每天可售出120千克.通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系.
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)当销售单价为何值时,该水果店销售这种水果每天获取的利润达到280元?
(3)水果店在进货成本不超过720元时,销售单价定为多少元可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表:
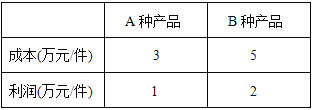
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)条件下,哪种方案获利最大?并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个等腰直角三角形△ABC和△CDE中,∠ACB=∠DCE=90°,AB=13![]() ,CD=5
,CD=5![]() ,△CDE绕点C在平面内自由旋转,当A、E、D三点共线时,AD的长是______.
,△CDE绕点C在平面内自由旋转,当A、E、D三点共线时,AD的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
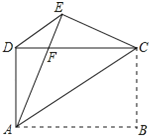
(1)求证:△DEC≌△EDA;
(2)求DF的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图1,在平面直角坐标系中,点![]() 是坐标原点,点
是坐标原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 是菱形,直线
是菱形,直线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.

(1)点![]() 的坐标是______;
的坐标是______;
(2)求直线![]() 的函数解析式;
的函数解析式;
(3)如图2,动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以1个单位长度/秒的速度向终点
方向以1个单位长度/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() (
(![]() ),点
),点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式(要求写出自变量
之间的函数关系式(要求写出自变量![]() 的取值范围)
的取值范围)
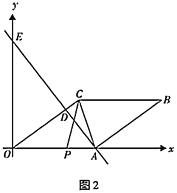
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com