
 如图,在Rt△ABC中,∠BAC=90°,AG⊥BC于G,BD平分∠ABC,AE⊥BD于H,交BC于E,AG交BD于F,连接EF.求证:
如图,在Rt△ABC中,∠BAC=90°,AG⊥BC于G,BD平分∠ABC,AE⊥BD于H,交BC于E,AG交BD于F,连接EF.求证:分析 (1)证得△ABH≌△EBH,根据全等三角形的性质即可证得结论;
(2)根据线段垂直平分线上的点到两端点的距离相等可得AF=EF,根据等角的余角相等求出∠ADB=∠AFD,再根据等角对等边可得AF=AD,然后等量代换即可得证.
解答 证明:(1)∵BD平分∠ABC,
∴∠ABH=∠EBH,
∵AE⊥BD,
∴∠AHB=∠BHE,
在△ABH和△EBH中
$\left\{\begin{array}{l}{∠ABH=∠EBH}\\{BH=BH}\\{∠AHB=∠BHE}\end{array}\right.$
∴△ABH≌△EBH(ASA),
∴AH=EH;
(2)∵BH为AE的垂直平分线,
∴AF=EF,
∵BD平分∠ABC,
∴∠DBC=∠ABD,
∵AG⊥BC,AE⊥BD,
∴∠ABD+∠ADB=90°,∠DBC+∠BFG=90°,
∴∠ADB=∠BFG,
∵∠AFD=∠BFG,
∴∠ADB=∠AFD,
∴AF=AD,
又∵AF=EF,
∴AD=EF.
点评 本题考查了角平分线上的性质,线段垂直平分线上的点到两端点的距离相等的性质,等角对等边的性质,熟记各性质并准确识图是解题的关键.


科目:初中数学 来源: 题型:解答题
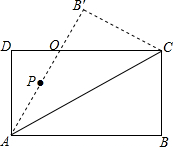 如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.
如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC为一个直角三角形的空地,∠C为直角,AC边长为3百米,BC边长为4百米,现决定在空地内筑一条笔直的路EF(宽度不计),E为BC的中点,F为三角形ABC边上的一点,且EF将该空地分成一个四边形和一个三角形,若分成的四边形和三角形周长相等,求此时小路EF的长度.
如图,△ABC为一个直角三角形的空地,∠C为直角,AC边长为3百米,BC边长为4百米,现决定在空地内筑一条笔直的路EF(宽度不计),E为BC的中点,F为三角形ABC边上的一点,且EF将该空地分成一个四边形和一个三角形,若分成的四边形和三角形周长相等,求此时小路EF的长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com