
ЁОЬтФПЁПМИКЮЬНОПЬт
(1)ЗЂЯжЃКдкЦНУцФкЃЌШєBCЃНaЃЌACЃНbЃЌЦфжаaЃОbЃЎ
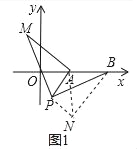
ЕБЕуAдкЯпЖЮBCЩЯЪБ(ШчЭМ1)ЃЌЯпЖЮABЕФГЄШЁЕУзюаЁжЕЃЌзюаЁжЕЮЊЁЁ ЁЁЃЛ
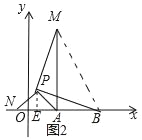
ЕБЕуAдкЯпЖЮBCбгГЄЯпЩЯЪБ(ШчЭМ2)ЃЌЯпЖЮABЕФГЄШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊЁЁ ЁЁЃЎ
(2)гІгУЃКЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌШчЭМ3ЃЌЗжБ№вдABЁЂACЮЊБпЃЌзїЕШБпЁїABDКЭЕШБпЁїACEЃЌСЌНгCDЁЂBEЃЎ
ЂйжЄУїЃКCDЃНBEЃЛ
ЂкШєBCЃН3ЃЌACЃН1ЃЌдђЯпЖЮCDГЄЖШЕФзюДѓжЕЮЊЁЁ ЁЁЃЎ
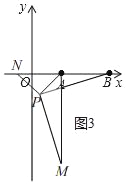
(3)ЭиеЙЃКШчЭМ4ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊ(2ЃЌ0)ЃЌЕуBЕФзјБъЮЊ(5ЃЌ0)ЃЌЕуPЮЊЯпABЭтвЛЖЏЕуЃЌЧвPAЃН2ЃЌPMЃНPBЃЌЁЯBPMЃН90ЁуЃЎЧыжБНгаДГіЯпЖЮAMГЄЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЎ

ЁОД№АИЁП(1)aЉbЃЛ a+bЃЛ(2)ЂйжЄУїМћНтЮіЃЛЂк4ЃЛ(3)ТњзуЬѕМўЕФЕуPзјБъ(2Љ![]() ЃЌ
ЃЌ![]() )Лђ(2Љ
)Лђ(2Љ![]() ЃЌЉ
ЃЌЉ![]() )ЃЌAMЕФзюДѓжЕЮЊ2
)ЃЌAMЕФзюДѓжЕЮЊ2![]() +3ЃЎ
+3ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕуAЮЛгкЯпЖЮBCЩЯЪБЃЌЯпЖЮABЕФГЄШЁЕУзюаЁжЕЃЌИљОнЕуAЮЛгкBCЕФбгГЄЯпЩЯЪБЃЌЯпЖЮABЕФГЄШЁЕУзюДѓжЕЃЌМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉЂйИљОнЕШБпШ§НЧаЮЕФаджЪЕУЕНADЃНABЃЌACЃНAEЃЌЁЯBADЃНЁЯCAEЃН60ЁуЃЌЭЦГіЁїCADЁеЁїEABЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНCDЃНBEЃЛ
ЂкгЩгкЯпЖЮCDГЄЕФзюДѓжЕЃНЯпЖЮBEЕФзюДѓжЕЃЌИљОнЃЈ1ЃЉжаЕФНсТлМДПЩЕУЕННсЙћЃЛ
ЃЈ3ЃЉНЋЁїAPMШЦзХЕуPЫГЪБеыа§зЊ90ЁуЕУЕНЁїPBNЃЌСЌНгANЃЌЕУЕНЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНPNЃНPAЃН2ЃЌBNЃНAMЃЌИљОнЕБNдкЯпЖЮBAЕФбгГЄЯпЪБЃЌЯпЖЮBNШЁЕУзюДѓжЕЃЌМДПЩЕУЕНзюДѓжЕЮЊ2![]() +3ЃЛШчЭМ2ЃЌЙ§PзїPEЁЭxжсгкEЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЎ
+3ЃЛШчЭМ2ЃЌЙ§PзїPEЁЭxжсгкEЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЎ
(1)ЁпЕБЕуAдкЯпЖЮBCЩЯЪБЃЌЯпЖЮABЕФГЄШЁЕУзюаЁжЕЃЌзюаЁжЕЮЊBCЉACЃЌЁпBCЃНaЃЌACЃНbЃЌЁрBCЉACЃНaЉbЃЌ
ЕБЕуAдкЯпЖЮBCбгГЄЯпЩЯЪБЃЌЯпЖЮABЕФГЄШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊBC+ACЃЌЁпBCЃНaЃЌACЃНbЃЌЁрBC+ACЃНa+bЃЌ
ЙЪД№АИЮЊЃКaЉbЃЌa+bЃЛ
(2)ЂйЁпЁїABDКЭЁїACEЪЧЕШБпШ§НЧаЮЃЌ
ЁрADЃНABЃЌACЃНAEЃЌЁЯBADЃНЁЯCAEЃН60ЁуЃЌ
ЁрЁЯDACЃНЁЯBAEЃЌ
дкЁїACDКЭЁїAEBжаЃЌ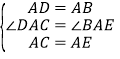 ЃЌ
ЃЌ
ЁрЁїACDЁеЁїAEB(SAS)ЃЌ
ЁрCDЃНBEЃЛ
ЂкЁпЯпЖЮCDЕФзюДѓжЕЃНЯпЖЮBEГЄЕФзюДѓжЕЃЌ
гЩ(1)жЊЃЌЕБЯпЖЮBEЕФГЄШЁЕУзюДѓжЕЪБЃЌЕуEдкBCЕФбгГЄЯпЩЯЃЌ
ЁрзюДѓжЕЮЊBC+CEЃНBC+ACЃН4ЃЌ
ЙЪД№АИЮЊЃК4ЃЛ
(3)ЁпНЋЁїAPMШЦзХЕуPЫГЪБеыа§зЊ90ЁуЕУЕНЁїPBNЃЌСЌНгANЃЌ
дђЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрPNЃНPAЃН2ЃЌBNЃНAMЃЌ
ЁпAЕФзјБъЮЊ(2ЃЌ0)ЃЌЕуBЕФзјБъЮЊ(5ЃЌ0)ЃЌ
ЁрOAЃН2ЃЌOBЃН5ЃЌ
ЁрABЃН3ЃЌ
ЁрЯпЖЮAMГЄЕФзюДѓжЕЃНЯпЖЮBNГЄЕФзюДѓжЕЃЌ
ЁрЕБNдкЯпЖЮBAЕФбгГЄЯпЪБЃЌЯпЖЮBNШЁЕУзюДѓжЕЃЌ
зюДѓжЕЃНAB+ANЃЌ
ЁпANЃН![]() APЃН2
APЃН2![]() ЃЌ
ЃЌ
ЁрзюДѓжЕЮЊ2![]() +3ЃЛ
+3ЃЛ
ШчЭМ2ЃЌЙ§PзїPEЁЭxжсгкEЃЌСЌНгBEЃЌ
ЁпЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрPEЃНAEЃН![]() ЃЌ
ЃЌ
ЁрOEЃНBOЉABЉAEЃН5Љ3Љ![]() ЃН2Љ
ЃН2Љ![]() ЃЌ
ЃЌ
ЁрP(2Љ![]() ЃЌ
ЃЌ![]() )ЃЎ
)ЃЎ
ШчЭМ3жаЃЌИљОнЖдГЦадПЩжЊЃЌЕБЕуPдкЕкЫФЯѓЯоЪБЃЌP(2Љ![]() ЃЌЉ
ЃЌЉ![]() )ЪБЃЌвВТњзуЬѕМўЃЎ
)ЪБЃЌвВТњзуЬѕМўЃЎ
злЩЯЪіЃЌТњзуЬѕМўЕФЕуPзјБъ(2Љ![]() ЃЌ
ЃЌ![]() )Лђ(2Љ
)Лђ(2Љ![]() ЃЌЉ
ЃЌЉ![]() )ЃЌAMЕФзюДѓжЕЮЊ2
)ЃЌAMЕФзюДѓжЕЮЊ2![]() +3ЃЎ
+3ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЪЧЕШБпШ§НЧаЮЃЌЕуDЪЧжБЯпBCЩЯвЛЕуЃЌвдADЮЊвЛБпдкADЕФгвВрзїЕШБп
ЪЧЕШБпШ§НЧаЮЃЌЕуDЪЧжБЯпBCЩЯвЛЕуЃЌвдADЮЊвЛБпдкADЕФгвВрзїЕШБп![]() ЃЎ
ЃЎ
![]() ШчЭМ
ШчЭМ![]() ЃЌЕуDдкЯпЖЮBCЩЯвЦЖЏЪБЃЌжБНгаДГі
ЃЌЕуDдкЯпЖЮBCЩЯвЦЖЏЪБЃЌжБНгаДГі![]() КЭ
КЭ![]() ЕФДѓаЁЙиЯЕЃЛ
ЕФДѓаЁЙиЯЕЃЛ
![]() ШчЭМ
ШчЭМ![]() ЭМ
ЭМ![]() ЃЌЕуDдкЯпЖЮBCЕФбгГЄЯпЩЯЛђЗДЯђбгГЄЯпЩЯвЦЖЏЪБЃЌВТЯы
ЃЌЕуDдкЯпЖЮBCЕФбгГЄЯпЩЯЛђЗДЯђбгГЄЯпЩЯвЦЖЏЪБЃЌВТЯы![]() ЕФДѓаЁЪЧЗёЗЂЩњБфЛЏЃЌШєВЛБфЧыжБНгаДГіНсТлВЂбЁдёЦфжавЛжжЭМЪОНјаажЄУїЃЛШєБфЛЏЃЌЧыЗжБ№аДГіЭМ
ЕФДѓаЁЪЧЗёЗЂЩњБфЛЏЃЌШєВЛБфЧыжБНгаДГіНсТлВЂбЁдёЦфжавЛжжЭМЪОНјаажЄУїЃЛШєБфЛЏЃЌЧыЗжБ№аДГіЭМ![]() ЁЂЭМ
ЁЂЭМ![]() ЫљЖдгІЕФНсТлЃЎ
ЫљЖдгІЕФНсТлЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзлКЯЬт
ЃЈ1ЃЉЁОЮЪЬтЬсГіЁПШчЭМ1ЃЎЁїABCЪЧЕШБпШ§НЧаЮЃЌЕуDдкЯпЖЮABЩЯЃЎЕуEдкжБЯпBCЩЯЃЎЧвЁЯDEC=ЁЯDCEЃЎЧѓжЄЃКBE=ADЃЛ
ЃЈ2ЃЉЁОРрБШбЇЯАЁПШчЭМ2ЃЎНЋЬѕМўЁАЕуDдкЯпЖЮABЩЯЁБИФЮЊЁАЕуDдкЯпЖЮABЕФбгГЄЯпЩЯЁБЃЌЦфЫћЬѕМўВЛБфЃЎХаЖЯЯпЖЮABЃЌBEЃЌBDжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЁОРЉеЙЬНОПЁПШчЭМ3ЃЎЁїABCЪЧЕШбќШ§НЧаЮЃЌAB=ACЃЌЁЯBAC=120ЁуЃЌЕуDдкЯпЖЮABЕФЗДЯђбгГЄЯпЩЯЃЌЕуEдкжБЯпBCЩЯЃЌЧвЁЯDEC=ЁЯDCEЃЌЁОРрБШбЇЯАЁПжаЕФЯпЖЮABЁЂBEЁЂBDжЎМфЕФЪ§СПЙиЯЕЪЧЗёЛЙГЩСЂЃПШєГЩСЂЃЌЧыЫЕУїРэгЩЃЛШєВЛГЩСЂЃЌЧыжБНгаДГіЯпЖЮABЃЌBEЃЌBDжЎМфЕФЪ§СПЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁППДЭМЬюПеЃКвбжЊШчЭМЃЌADЁЭBCгкDЃЌEGЁЭBCгкGЃЌЁЯE=ЁЯ1ЃЌ
ЧѓжЄЃКADЦНЗжЁЯBACЃЎ
жЄУїЃКЁпADЁЭBCгкDЃЌEGЁЭBCгкGЃЈ вбжЊ ЃЉ
ЁрЁЯADC=90ЁуЃЌЁЯEGC=90ЁуЃЈ___________ЃЉ
ЁрЁЯADC=ЁЯEGCЃЈЕШСПДњЛЛЃЉ
ЁрADЁЮEGЃЈ_____________ЃЉ
ЁрЁЯ1=ЁЯ2ЃЈ___________ЃЉ
ЁЯE=ЁЯ3ЃЈ___________ЃЉ
гжЁпЁЯE=ЁЯ1ЃЈ вбжЊЃЉ
ЁрЁЯ2=ЁЯ3ЃЈ___________ЃЉ
ЁрADЦНЗжЁЯBACЃЈ___________ЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЮхвЛРЭЖЏНкДѓГъБіЃЁЁБЃЌФГЩЬГЁЩшМЦЕФДйЯњЛюЖЏШчЯТЃКдквЛИіВЛЭИУїЕФЯфзгРяЗХга4ИіЯрЭЌЕФаЁЧђЃЌЧђЩЯЗжБ№БъгаЁА0дЊЁБЁЂЁА10дЊЁБЁЂЁА20дЊЁБКЭЁА50дЊЁБЕФзжбљЃЎЙцЖЈЃКдкБОЩЬГЁЭЌвЛШеФкЃЌЙЫПЭУПЯћЗбТњ300дЊЃЌОЭПЩвддкЯфзгРяЯШКѓУўГіСНИіЧђЃЈЕквЛДЮУўГіКѓВЛЗХЛиЃЉЃЎЩЬГЁИљОнСНаЁЧђЫљБъН№ЖюЕФКЭЗЕЛЙЯрЕШМлИёЕФЙКЮяШЏЃЌЙКЮяШЏПЩвддкБОЩЬГЁЯћЗбЃЎФГЙЫПЭИеКУЯћЗб300дЊЃЎ
ЃЈ1ЃЉИУЙЫПЭжСЖрПЩЕУЕНдЊЙКЮяШЏЃЛ
ЃЈ2ЃЉЧыФугУЛЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓГіИУЙЫПЭЫљЛёЕУЙКЮяШЏЕФН№ЖюВЛЕЭгк50дЊЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЕФЦпБпаЮABCDEFGжаЃЌABЁЂEDЕФбгГЄЯпЯрНЛгкOЕуЃЎШєЭМжаЁЯ1ЁЂЁЯ2ЁЂЁЯ3ЁЂЁЯ4ЕФЭтНЧЕФНЧЖШКЭЮЊ220ЁуЃЌдђЁЯBODЕФЖШЪ§ЪЧЃЈЁЁЁЁЃЉ

A. 400 B. 450 C. 500 D. 600
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЕуDЪЧЁїABCЫљдкЦНУцФквЛЕуЃЌСЌНгADЁЂCDЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєЁЯAЃН28ЁуЃЌЁЯBЃН72ЁуЃЌЁЯCЃН11ЁуЃЌЧѓЁЯADCЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєДцдквЛЕуPЃЌЪЙЕУPBЦНЗжЁЯABCЃЌЭЌЪБPDЦНЗжЁЯADCЃЌЬНОПЁЯAЃЌЁЯPЃЌЁЯCЕФЙиЯЕВЂжЄУїЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдк ЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋЕуDвЦжСЁЯABCЕФЭтВПЃЌЦфЫќЬѕМўВЛБфЃЌЬНОПЁЯAЃЌЁЯPЃЌЁЯCЕФЙиЯЕВЂжЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхвЛжжаТдЫЫуЁАaЁюbЁБЕФКЌвхЮЊЃКЕБaЁнbЪБЃЌaЁюb=a+bЃЛЕБaЃМbЪБЃЌaЁюb=a-bЃЎР§ШчЃК3ЁюЃЈ-4ЃЉ=3+ЃЈ-4ЃЉ=-1ЃЌЃЈ-6ЃЉЁю![]() =-6-
=-6-![]() =-6
=-6![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЬюПеЃКЃЈ-4ЃЉЁю3=______ЃЛ
ЃЈ2ЃЉШчЙћЃЈ3x-4ЃЉЁюЃЈ2x+8ЃЉ=ЃЈ3x-4ЃЉ-ЃЈ2x+8ЃЉЃЌЧѓxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШчЙћЃЈ3x-7ЃЉЁюЃЈ3-2xЃЉ=2ЃЌЧѓxЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТБэЪЧщйзгЕФЯњЪлЖюЫцщйзгТєГіжЪСПЕФБфЛЏБэЃК
жЪСП/ЧЇПЫ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Ё |
ЯњЪлЖю/дЊ | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | Ё |
ЃЈ1ЃЉетИіБэЗДгГСЫФФСНИіБфСПжЎМфЕФЙиЯЕЃПФФИіЪЧздБфСПЃПФФИіЪЧвђБфСПЃП
ЃЈ2ЃЉЕБщйзгТєГі5ЧЇПЫЪБЃЌЯњЪлЖюЪЧ_______дЊ.
ЃЈ3ЃЉШчЙћгУ![]() БэЪОщйзгТєГіЕФжЪСПЃЌ
БэЪОщйзгТєГіЕФжЪСПЃЌ![]() БэЪОЯњЪлЖюЃЌАДБэжаИјГіЕФЙиЯЕЃЌ
БэЪОЯњЪлЖюЃЌАДБэжаИјГіЕФЙиЯЕЃЌ![]() гы
гы![]() жЎМфЕФЙиЯЕЪНЮЊ______.
жЎМфЕФЙиЯЕЪНЮЊ______.
ЃЈ4ЃЉЕБщйзгЕФЯњЪлЖюЪЧ100дЊЪБЃЌЙВТєГіЖрЩйЧЇПЫщйзгЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com