
【题目】△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( )
A.2cm,2cm,2cmB.3cm,3cm,3cmC.4cm,4cm,4cmD.2cm,3cm,5cm
【答案】A
【解析】
连接OA,OB,OC,利用角的平分线上的点到角的两边的距离相等可知△BDO≌△BFO,△CDO≌△CEO,△AEO≌△AFO,所以BD=BF,CD=CE,AE=AF,又因为点O到三边AB、AC、BC的距离是CD,所以AB=8-CD+6-CD=10,解得CD=2,所以点O到三边AB、AC、BC的距离为2.
连接OA,OB,OC,则△BDO≌△BFO,△CDO≌△CEO,△AEO≌△AFO,
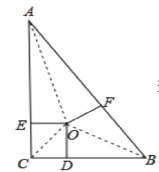
∴BD=BF,CD=CE,AE=AF,
又∵∠C=90°,OD⊥BC于D,OE⊥AC于E,且O为△ABC三条角平分线的交点
∴四边形OECD是正方形,
则点O到三边AB、AC、BC的距离=CD,
∴AB=8CD+6CD=2CD+14,又根据勾股定理可得:AB=10,
即2CD+14=10
∴CD=2,
即点O到三边AB、AC、BC的距离为2cm.
故选A


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,O是直线![]() 上一点,
上一点,![]() 是一条射线,
是一条射线,![]() 平分
平分![]() ,
,![]() 在
在![]() 内,
内,![]() .
.
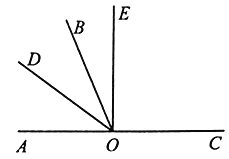
(1)若![]() ,垂足为O点,则
,垂足为O点,则![]() 的度数为________°,
的度数为________°,![]() 的度数为________°;在图中,与
的度数为________°;在图中,与![]() 相等的角有_________;
相等的角有_________;
(2)若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是正方形网格中的三个格点.
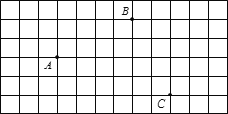
(1)①画射线AC;
②画线段BC;
③过点B画AC的平行线BD;
④在射线AC上取一点E,画线段BE,使其长度表示点B到AC的距离;
(2)在(1)所画图中,
①BD与BE的位置关系为 ;
②线段BE与BC的大小关系为BE BC(填“>”、“<”或“=”),理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题引入】
已知:如图BE、CF是ΔABC的中线,BE、CF相交于G。求证: ![]()
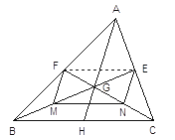
证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BF且EF=![]() BC
BC
∴![]()
【思考解答】
(1)连结AG并延长AG交BC于H,点H是否为BC中点 (填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN 是 四边形。
②当![]() 的值为 时,四边形EFMN 是矩形。
的值为 时,四边形EFMN 是矩形。
③当![]() 的值为 时,四边形EFMN 是菱形。
的值为 时,四边形EFMN 是菱形。
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积![]() =_________
=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
由于发展时间早、发展速度快,经过20多年大规模的高速开发建设,北京四环内,甚至五环内可供开发建设的土地资源越来越稀缺,更多的土地供应将集中在五环外,甚至六环外的远郊区县.
据中国经济网2017年2月报道,来自某市场研究院的最新统计,2016年,剔除了保障房后,在北京新建商品住宅交易量整体上涨之时,北京各区域的新建商品住宅交易量则是有涨有跌![]() 其中,昌平、通州、海淀、朝阳、西城、东城六区下跌,跌幅最大的为朝阳区,新建商品住宅成交量比2015年下降了
其中,昌平、通州、海淀、朝阳、西城、东城六区下跌,跌幅最大的为朝阳区,新建商品住宅成交量比2015年下降了![]() 而延庆、密云、怀柔、平谷、门头沟、房山、顺义、大兴、石景山、丰台十区的新建商品住宅成交量表现为上涨,涨幅最大的为顺义区,比2015年上涨了
而延庆、密云、怀柔、平谷、门头沟、房山、顺义、大兴、石景山、丰台十区的新建商品住宅成交量表现为上涨,涨幅最大的为顺义区,比2015年上涨了![]() 另外,从环线成交量的占比数据上,同样可以看出成交日趋郊区化的趋势
另外,从环线成交量的占比数据上,同样可以看出成交日趋郊区化的趋势![]() 根据统计,2008年到2016年,北京全市成交的新建商品住宅中,二环以内的占比逐步从
根据统计,2008年到2016年,北京全市成交的新建商品住宅中,二环以内的占比逐步从![]() 下降到了
下降到了![]() ;二、三环之间的占比从
;二、三环之间的占比从![]() 下降到了
下降到了![]() ;三、四环之间的占比从
;三、四环之间的占比从![]() 下降到了
下降到了![]() ;四、五环之间的占比从
;四、五环之间的占比从![]() 下降到了
下降到了![]() 也就是说,整体成交中位于五环之内的新房占比,从2008年的
也就是说,整体成交中位于五环之内的新房占比,从2008年的![]() 下降到了2016年的
下降到了2016年的![]() ,下滑趋势非常明显
,下滑趋势非常明显![]() 由此可见,新房市场的远郊化是北京房地产市场发展的大势所趋
由此可见,新房市场的远郊化是北京房地产市场发展的大势所趋![]() 注:占比,指在总数中所占的比重,常用百分比表示
注:占比,指在总数中所占的比重,常用百分比表示![]()
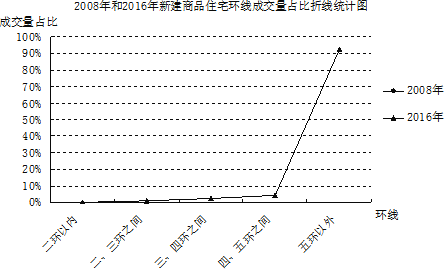
根据以上材料解答下列问题:
![]() 补全折线统计图;
补全折线统计图;
![]() 根据材料提供的信息,预估2017年位于北京市五环之内新建商品住宅成交量占比约______ ,你的预估理由是______ .
根据材料提供的信息,预估2017年位于北京市五环之内新建商品住宅成交量占比约______ ,你的预估理由是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,![]() 的顶点坐标分别是
的顶点坐标分别是![]() ,对于
,对于![]() 的横长、纵长、纵横比给出如下定义:
的横长、纵长、纵横比给出如下定义:
将![]() 中的最大值,称为
中的最大值,称为![]() 的横长,记作
的横长,记作![]() ;将
;将![]() 中的最大值,称为
中的最大值,称为![]() 的纵长,记作
的纵长,记作![]() ;将
;将![]() 叫做
叫做![]() 的纵横比,记作
的纵横比,记作![]() .
.
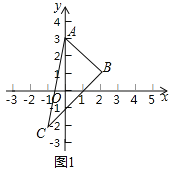
例如:如图![]() 的三个顶点的坐标分别是
的三个顶点的坐标分别是![]() ,则
,则![]() ,
,
所以![]() .
.
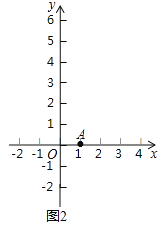
![]() 如图2,点
如图2,点![]() ,
,
![]() 点
点![]() ,
,
则![]() 的纵横比
的纵横比![]() ______
______
![]() 的纵横比
的纵横比![]() ______;
______;
![]() 点F在第四象限,若
点F在第四象限,若![]() 的纵横比为1,写出一个符合条件的点F的坐标;
的纵横比为1,写出一个符合条件的点F的坐标;
![]() 点M是双曲线
点M是双曲线![]() 上一个动点,若
上一个动点,若![]() 的纵横比为1,求点M的坐标;
的纵横比为1,求点M的坐标;
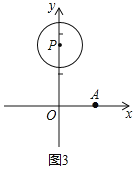
![]() 如图3,点
如图3,点![]() 以
以![]() 为圆心,1为半径,点N是
为圆心,1为半径,点N是![]() 上一个动点,直接写出
上一个动点,直接写出![]() 的纵横比
的纵横比![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.有且只有一条直线与已知直线垂直;
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线距离;
C.互相垂直的两条线段一定相交;
D.直线![]() 外一点
外一点![]() 与直线
与直线![]() 上各点连接而成的所有线段中,最短线段的长度是
上各点连接而成的所有线段中,最短线段的长度是![]() ,则点
,则点![]() 到直线
到直线![]() 的距离是
的距离是![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD= ![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
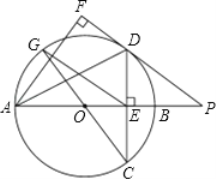
【题目】如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG.
(1)求证:DF是⊙O的切线;
(2)若AD=DP,OB=3,求![]() 的长度;
的长度;
(3)若DE=4,AE=8,求线段EG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com