
【题目】如图,O是直线![]() 上一点,
上一点,![]() 是一条射线,
是一条射线,![]() 平分
平分![]() ,
,![]() 在
在![]() 内,
内,![]() .
.
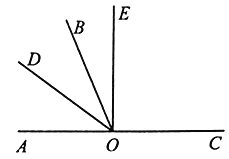
(1)若![]() ,垂足为O点,则
,垂足为O点,则![]() 的度数为________°,
的度数为________°,![]() 的度数为________°;在图中,与
的度数为________°;在图中,与![]() 相等的角有_________;
相等的角有_________;
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)30,30,∠EOD;(2)87°
【解析】
(1)根据![]() ,即可得到∠BOE,然后求出∠AOB,利用角平分线的定义求出∠BOD,再然后根据求出∠EOD的度数,与∠AOB相等;
,即可得到∠BOE,然后求出∠AOB,利用角平分线的定义求出∠BOD,再然后根据求出∠EOD的度数,与∠AOB相等;
(2)根据角平分线的定义求出∠AOB,再求出∠BOC,然后求解即可.
解:(1)∵![]() ,O是直线
,O是直线![]() 上一点
上一点
∴∠EOC=∠AOE=90°
又∵![]()
∴![]()
∴∠AOB=90°-30°=60°
∵![]() 平分
平分![]()
∴![]()
∵∠EOD=∠BOD+∠BOE=60°
所依∠AOB=∠EOD
故答案为:30,30,∠EOD;
(2)因为OD平分∠AOB,所以∠AOB=2∠AOD.
因为∠AOD=32°,所以∠AOB=64°.
所以∠COB=180°-∠AOB =116°.
因为∠BOE=![]() ∠EOC,
∠EOC,
所以∠EOC=![]() ∠COB=
∠COB=![]() =87°.
=87°.


科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,点![]() 、
、![]() 、
、![]() 是三个格点(网格线的交点叫做格点)
是三个格点(网格线的交点叫做格点)
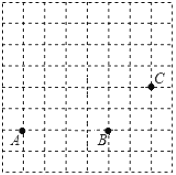
(1)画线段![]() ,画射线
,画射线![]() ,过点
,过点![]() 画
画![]() 的平行线
的平行线![]() ;
;
(2)过点![]() 画直线
画直线![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,则点
,则点![]() 到
到![]() 的距离是线段______的长度;
的距离是线段______的长度;
(3)线段![]() ______线段
______线段![]() (填“>”或“<”),理由是______.
(填“>”或“<”),理由是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的内切圆.
(1)若∠A=60°,连接BO、CO并延长,分别交AC、AB于点D、E,
① 求∠BOC的度数;
② 试探究BE、CD、BC之间的等量关系,并证明你的结论;
(2)若AB=AC=10,sin∠ABC=![]() ,AC、AB与⊙O相切于点D、E,将BC向上平移与⊙O交于点F、G,若以D、E、F、G为顶点的四边形是矩形,求平移的距离.
,AC、AB与⊙O相切于点D、E,将BC向上平移与⊙O交于点F、G,若以D、E、F、G为顶点的四边形是矩形,求平移的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=m(m为常数),点C为直线AB上一点(不与点A、B重合),点M、N分别在线段BC、AC上,且满足CN=3AN,CM=3BM.
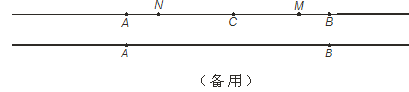
(1)如图,当点C恰好在线段AB中点,且m=8时,则MN=______;
(2) 若点C在点A左侧,同时点M在线段AB上(不与端点重合),请判断CN+2AM -2MN的值是否与m有关?并说明理由.
(3) 若点C是直线AB上一点(不与点A、B重合),同时点M在线段AB上(不与端点重合),求MN长度 (用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程是刻画现实世界的有效模型,表格是建立方程的策略之一.请填写表格数据,并列方程解决问题.轮船和汽车都从甲地开往乙地,海路比公路近40千米,轮船上午7点开出,速度是每小时24千米.汽车上午10点开出,速度为每小时40千米,结果同时到达了乙地.求甲、乙两地的海路和公路长.
速度 | 时间 | 路程 | |
汽车 | 40 |
| x |
轮船 | 24 |
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次篮球联赛中,两队的积分如下表所示:
队名 | 比赛场次 | 胜场场次 | 负场场次 | 积分 |
前进 | 14 | 10 | 4 | 24 |
钢铁 | 14 | 0 | 14 | 14 |
请回答下列问题:
(1)负一场_________积分;
(2)求胜一场积多少分?
(3)某队的胜场总积分比负场总积分的3倍多3分,求该队胜了多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】父亲带着两个儿子向离家33千米的奶奶家出发,父亲有一辆摩托车,速度为25千米![]() 小时,如果再载了另一个人,则速度为20千米
小时,如果再载了另一个人,则速度为20千米![]() 小时
小时![]() 摩托车不允许带两个人,即每车至多载两人
摩托车不允许带两个人,即每车至多载两人![]() 每个儿子如果步行速度为5千米
每个儿子如果步行速度为5千米![]() 小时,为尽快到达奶奶家,出发时,父亲让第二个儿子先步行,将第一个儿子载了一段路程后让其步行前往奶奶家,并立即返回接步行的第二个儿子,结果与第一个儿子同时到达奶奶家,则在路上共计用的时间为______小时.
小时,为尽快到达奶奶家,出发时,父亲让第二个儿子先步行,将第一个儿子载了一段路程后让其步行前往奶奶家,并立即返回接步行的第二个儿子,结果与第一个儿子同时到达奶奶家,则在路上共计用的时间为______小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( )
A.2cm,2cm,2cmB.3cm,3cm,3cmC.4cm,4cm,4cmD.2cm,3cm,5cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com