
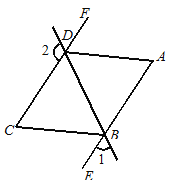
【题目】如图12,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与CF平行吗?请说明理由;
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:
(1)AE∥CF,理由如下:
∵ ∠CDB+∠2=180°, ( 平角的定义 )
∠1+∠2=180°, ( 已知 )
∴ ∠1=∠ , ( )
∴ AE∥CF. ( )
(2)AD与BC的位置关系是: .
∵ AE∥CF,( 已知 )
∴ ∠C=∠ .( )
又∵ ∠A=∠C,( 已知 )
∴ ∠A=∠CBE . ( )
∴ ∥ .( )
(3)
【答案】(1)AE∥CF, (2)AD与BC的位置关系是:AD∥BC(3)BC平分∠DBE,
【解析】试题分析:(1)证明∠1=∠ CDB ,利用同位角相等,两直线平行即可证得;
(2)根据平行线的性质可得∠A=∠CBE,然后利用平行线的判定方法即可证得;
(3)根据平行线的性质即可得∠EBC=∠CBD,由DA平分∠BDF可得∠ADB=![]() ∠BDF,再由等量代换得 ∠CBD=
∠BDF,再由等量代换得 ∠CBD=![]() ∠DBE,从而结论得证.
∠DBE,从而结论得证.
解:(1)AE∥CF,理由如下:
∵ ∠CDB+∠2=180°, ( 平角的定义 )
∠1+∠2=180°,
∴ ∠1=∠ CDB , ( 同角的补角相等 )
∴ AE∥CF. ( 同位角相等,两直线平行 )
(2)AD与BC的位置关系是:AD∥BC .
∵ AE∥CF, ( 已知 )
∴ ∠C=∠ CBE . ( 两直线平行,内错角相等 )
又∵ ∠A=∠C, ( 已知 )
∴ ∠A=∠CBE . ( 等量代换 )
∴ AD ∥ BC . ( 同位角相等,两直线平行 )
(3)BC平分∠DBE,理由如下:
由(1)知AB∥CF,
∴ ∠BDF=∠DBE.
由(2)知AD∥BC,
∴ ∠ADB=∠CBD.
∵ DA平分∠BDF,
∴ ∠ADB=![]() ∠BDF,
∠BDF,
∴ ∠CBD=![]() ∠DBE,
∠DBE,
∴ BC平分∠DBE.


科目:初中数学 来源: 题型:
【题目】下列事件是随机事件的是( )
A. 每周有7天
B. 袋中有三个红球,摸出一个球一定是红球
C. 在同一平面内,垂直于同一条直线的两条直线互相垂直
D. 任意购买一张车票,座位刚好靠窗口
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判定四边形ABCD为平行四边形的条件是( )
A. AB∥CD,AB=CD B. ∠A=∠C,∠B=∠D
C. AB=AD,BC=CD D. AB=CD,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, AC切⊙O于点A,且AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E,连接AP 、AF.
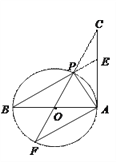
求证:(1)AF∥BE;(2)△ACP ∽△FCA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①要了解一批灯泡的使用寿命,应采用普查的方式;
②若一个游戏的中奖率是1%,则做100次这样的游戏一定会中奖;
③甲、乙两组数据的样本容量与平均数分别相同,若方差 ![]() =0.1,
=0.1, ![]() =0.2,则甲组数据比乙组数据稳定;
=0.2,则甲组数据比乙组数据稳定;
④“掷一枚硬币,正面朝上”是必然事件.
正确说法的序号是( )
A.①
B.②
C.③
D.④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com