
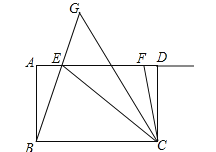
【题目】如图,在四边形ABCD中,AD//BC,点E在边AD上,且CB=CE,点F是射线ED上的一个动点,![]() 的平分线CG交BE的延长线于点G.
的平分线CG交BE的延长线于点G.
(1)若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)在动点F运动的过程中,![]() 的值是否发生变化?若不变,求出它的值;若变化 ,请说明理由.
的值是否发生变化?若不变,求出它的值;若变化 ,请说明理由.
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
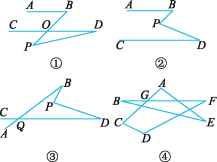
【题目】(1)如图①所示,若AB∥CD,点P在AB,CD外部,则有∠B=∠BOD.又因∠BOD是△POD的外角,故∠BOD=∠P+∠D,得∠P=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?并证明你的结论;
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E+∠F的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
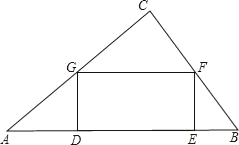
【题目】如图,在一块三角形区域ABC中,∠C=90°,边AC=8m,BC=6m,现要在△ABC内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上.
(1)求△ABC中AB边上的高h;
(2)设DG=x,当x取何值时,水池DEFG的面积(S)最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程x2+2x﹣m2﹣m=0(m>0),当m=1、2、3、…、2018时,相应的一元二次方程的两个根分别记为α1、β1,α2、β2,…,α2018、β2018,则:![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤SBDE:S△ACD=BD:AC,其中正确的个数( )
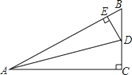
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市开展早市促销活动,为早到的顾客准备一份简易早餐,餐品为四样A:菜包、B:面包、C:鸡蛋、D:油条.超市约定:随机发放,早餐一人一份,一份两样,一样一个.
(1)按约定,“某顾客在该天早餐得到两个鸡蛋”是 事件(填“随机”、“必然”或“不可能”);
(2)请用列表或画树状图的方法,求出某顾客该天早餐刚好得到菜包和油条的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=2x﹣4的图象分別交x、y轴于点A、B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是_____.
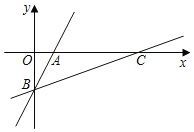
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求:汽车行驶中每千米用电费用是多少元?甲、乙两地的距离是多少千米?
(2)若汽车从甲地到乙地采用油电混合动力行驶,且所需费用不超过50元,则至少需要用电行驶多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com