
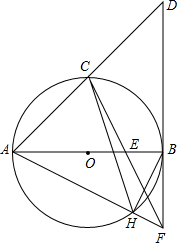
 如图,AB是⊙的直径,C是$\widehat{AB}$的中点,BD⊥AB交AC的延长线于点D,E是OB的中点,CE的延长线交DB于F,AF交⊙O于H,连接BH.
如图,AB是⊙的直径,C是$\widehat{AB}$的中点,BD⊥AB交AC的延长线于点D,E是OB的中点,CE的延长线交DB于F,AF交⊙O于H,连接BH.分析 (1)连接BC,由AB为直径,且C为弧AB的中点,利用圆周角定理及等弧对等弦,得到三角形ABC为等腰直角三角形,进而确定出三角形ABD为等腰直角三角形,利用三线合一得到AC=CD;
(2)利用等弧所对的圆周角相等即可求出∠AHC的度数;
(3)①连接OC,则OC⊥AB,证出OC∥DF,由E是OB的中点,得出BF=OC=OB,根据勾股定理求出AF,然后由△ABF的面积=$\frac{1}{2}$AB•BF=$\frac{1}{2}$AF•BH,即可求出BH;
②求出AC与AH的长,在三角形ACH中,利用余弦定理即可求出CH的长.
解答 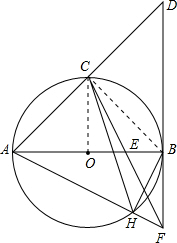 解:(1)连接BC,
解:(1)连接BC,
∵AB为圆O的直径,且C为$\widehat{AB}$的中点,
∴∠ACB=90°,AC=BC,
∴∠CAB=∠ABC=45°,
∵∠ABD=90°,
∴△ABD为等腰直角三角形,即AB=DB,
∵BC⊥AD,
∴C为AD的中点,
∴AC=CD;
(2)∵∠AHC与∠ABC都对$\widehat{AC}$,
∴∠AHC=∠ABC=45°;
(3)①连接OC,如图所示:
∵AC=BC,O为AB的中点,
∴OC⊥AB,
∴OC∥DF,
∵E是OB的中点,
∴BF=OC=OB=2,
∵∠ABF=90°,
∴AF=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∵△ABF的面积=$\frac{1}{2}$AB•BF=$\frac{1}{2}$AF•BH,
∴BH=$\frac{AB•BF}{AF}$=$\frac{4×2}{2\sqrt{5}}$=$\frac{4\sqrt{5}}{5}$;
②∵AC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=$\frac{8\sqrt{5}}{5}$,∠AHC=45°,
∴由余弦定理得:AC2=AH2+CH2-2AH•CH•cos45°,即8=$\frac{64}{5}$+CH2-$\frac{8\sqrt{10}}{5}$CH,
整理得:5CH2-8$\sqrt{10}$CH+24=0,
解得:CH=$\frac{8\sqrt{10}±\sqrt{640-480}}{10}$=$\frac{8\sqrt{10}±2\sqrt{10}}{10}$,即CH=$\sqrt{10}$或CH=$\frac{3\sqrt{10}}{5}$.
点评 此题属于圆的综合题,涉及的知识有:圆周角定理,等腰直角三角形的判定与性质,三线合一性质,勾股定理,三角形面积求法,以及余弦定理,熟练掌握定理及性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
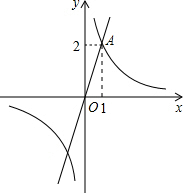 如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.
如图,已知点A(1,2)是正比例函数y1=kx(k≠0)与反比例函数y2=$\frac{m}{x}$(m≠0)的一个交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
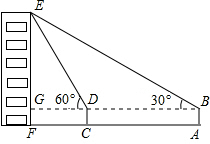 如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)
如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 李叔叔刚分到一套新房,其结构如图所示(单位:m),他打算除卧室外,其余部分铺地砖.
李叔叔刚分到一套新房,其结构如图所示(单位:m),他打算除卧室外,其余部分铺地砖. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com