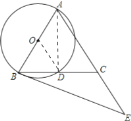
【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，点E在AC的延长线上，且∠CBE=
∠BAC．
（1）求证：BE是⊙O的切线；
（2）若∠ABC=65°，AB=6，求劣弧AD的长．
【答案】（1）证明见解析（2）
【解析】
（1）连接
，根据圆周角的性质求得
。根据等腰三角形的性质三效合一的性质得出
，进而根据已知条件即可证明
，从而证明
是
的切线；
（2）连接
，等腰三角形的性质和三角形外角的性质，求出
的度数，进而根据弧长公式即可求出.
（1）证明：如图，连接AD.
∵AB为直径，
∴∠ADB=90°，即AD⊥BC.
∵AB=AC，
∴∠BAD=∠CAD=
∠BAC.
∵∠CBE=∠BAC，
∴∠CBE=∠BAD.
∵∠BAD+∠ABD=90°，
∴∠ABE=∠ABD+∠CBE=90°.
∵AB为⊙O直径，
∴BE是⊙O的切线.
（2）解：如图，连接OD.
∵∠ABC=65°，
∴∠AOD=2∠ABC=2×65°=130°.
∵AB=6，
∴圆的半径为3.
∴劣弧AD的长为
=
.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】设a，b是任意两个不等实数，我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]．对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n时，有m≤y≤n，我们就称此函数是闭区间[m，n]上的“闭函数”．如函数y=﹣x+4，当x=1时，y=3；当x=3时，y=1，即当1≤x≤3时，恒有1≤y≤3，所以说函数y=﹣x+4是闭区间[1，3]上的“闭函数”，同理函数y=x也是闭区间[1，3]上的“闭函数”．
（1）反比例函数y=
是闭区间[1，2018]上的“闭函数”吗？请判断并说明理由；
（2）如果已知二次函数y=x2﹣4x+k是闭区间[2，t]上的“闭函数”，求k和t的值；
（3）如果（2）所述的二次函数的图象交y轴于C点，A为此二次函数图象的顶点，B为直线x=1上的一点，当△ABC为直角三角形时，写出点B的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在某住房小区的建设中，为了提高业主的宜居环境，小区准备在一个长为
米，宽为
米的长方形草坪上修建两条宽为
米的通道．
（1）剩余草坪的面积是多少平方米？
（2）当
，
时，剩余草坪的面积是多少平方米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知二次函数
的图象过A（2，0），B（0，-1）和C（4，5）三点。
（1）求二次函数的解析式；
（2）设二次函数的图象与
轴的另一个交点为D，求点D的坐标；
（3）在同一坐标系中画出直线
，并写出当在什么范围内时，一次函数的值大于二次函数的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等边△ABC边长为10，P在AB上，Q在BC延长线，CQ＝PA，过点P作PE⊥AC点E，过点P作PF∥BQ，交AC边于点F，连接PQ交AC于点D，则DE的长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=AC，射线AP在△ABC的外侧，点B关于AP的对称点为D，连接CD交射线AP于点E，连接BE.
(1)根据题意补全图形；
(2)求证：CD=EB+EC；
(3)求证：∠ABE=∠ACE.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=90° ，AC=3，BC=6，点D在AB上，AD=AC， AF⊥CD交CD于点E，交CB于点F，则CF的长是____.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xoy中，函数
的图象与一次函数y=kx－k的图象的交点为A（m，2）.
（1）求一次函数的解析式；
（2）设一次函数y=kx－k的图象与y轴交于点B，若P是x轴上一点， 且满足△PAB的面积是4，
直接写出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在ABCD中，DE平分∠ADB，交AB于E，BF平分∠CBD，交CD于F．
（1）求证：△ADE≌△CBF；
（2）当AD与BD满足什么关系时，四边形DEBF是矩形？请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com