
ЎҫМвДҝЎҝФД¶БАнҪвЈ¬ІўҪвҫцОКМвЈә
Ў°ХыМеЛјПлЎұКЗЦРС§КэС§ЦРөДТ»ЦЦЦШТӘЛјПлЈ¬№бҙ©УЪЦРС§КэС§өДИ«№эіМЈ¬ұИИзХыМеҙъИлЈ¬ХыМе»»ФӘЈ¬ХыМеФјјхЈ¬ХыМеЗуәНЈ¬ХыМе№№ФмЈ¬ЎӯЈ¬УРР©ОКМвИфҙУҫЦІҝЗуҪвЈ¬ІЙИЎёчёц»чЖЖөД·ҪКҪЈ¬әЬДСҪвҫцЈ¬¶шҙУИ«ҫЦЧЕСЫЈ¬ХыМеЛјҝјЈ¬»бК№ОКМв»Ҝ·ұОӘјтЈ¬»ҜДСОӘТЧЈ¬ёҙФУОКМвТІДЬУӯИР¶шҪвЈ®
АэЈәөұҙъКэКҪ![]() өДЦөОӘ7КұЈ¬ЗуҙъКэКҪ
өДЦөОӘ7КұЈ¬ЗуҙъКэКҪ![]() өДЦөЈ®
өДЦөЈ®
ҪвЈәТтОӘ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј®
Ј®
ЛщТФЈ®![]()
ТФЙП·Ҫ·ЁКЗөдРНөДХыМеҙъИл·ЁЈ®
ЗлёщҫЭФД¶БІДБПЈ¬ҪвҫцПВБРОКМвЈә
ЈЁ1Ј©ТСЦӘ![]() Ј¬Зу
Ј¬Зу![]() өДЦөЈ®
өДЦөЈ®
ЈЁ2Ј©ОТГЗЦӘөА·ҪіМ![]() өДҪвКЗ
өДҪвКЗ![]() Ј¬ПЦёшіцБнТ»ёц·ҪіМ
Ј¬ПЦёшіцБнТ»ёц·ҪіМ![]() Ј¬ФтЛьөДҪвКЗЎЎЎЎЎЎЎЎЈ®
Ј¬ФтЛьөДҪвКЗЎЎЎЎЎЎЎЎЈ®
 ФД¶БҝміөПөБРҙр°ё
ФД¶БҝміөПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
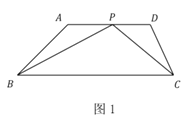
ЎҫМвДҝЎҝОКМвұіҫ°ЈәИзНјЈ¬ЛДұЯРО![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ОӘұЯ
ОӘұЯ![]() ЙПТ»¶ҜөгЈ¬Б¬ҪУ
ЙПТ»¶ҜөгЈ¬Б¬ҪУ![]() Ўў
Ўў![]() Ј®
Ј®
ОКМвМҪҫҝ
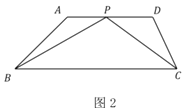
ЈЁ1Ј©ИзНј1Ј¬Иф![]() Ј¬Фт
Ј¬Фт![]() өДіӨОӘ__________Ј®
өДіӨОӘ__________Ј®
ЈЁ2Ј©ИзНј2Ј¬ЗлЗуіц![]() ЦЬіӨөДЧоРЎЦөЈ»
ЦЬіӨөДЧоРЎЦөЈ»
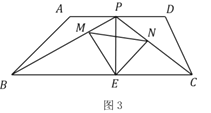
ЈЁ3Ј©ИзНј3Ј¬№эөг![]() Чч
Чч![]() УЪөг
УЪөг![]() Ј¬№эөг
Ј¬№эөг![]() ·ЦұрЧч
·ЦұрЧч![]() УЪ
УЪ![]() Ј¬
Ј¬![]() УЪөг
УЪөг![]() Ј¬Б¬ҪУ
Ј¬Б¬ҪУ![]()
ўЩКЗ·сҙжФЪөг![]() Ј¬К№өГ
Ј¬К№өГ![]() өДГж»эЧоҙуЈҝИфҙжФЪЈ¬Зуіц
өДГж»эЧоҙуЈҝИфҙжФЪЈ¬Зуіц![]() Гж»эөДЧоҙуЦөЈ¬ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ»
Гж»эөДЧоҙуЦөЈ¬ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ»
ўЪЗлЦұҪУРҙіц![]() Гж»эөДЧоРЎЦөЈ®
Гж»эөДЧоРЎЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҫШРО¶ФҪЗПЯөДЛДөИ·ЦөгҪРЧцҫШРОөДЖжМШөгЈ®ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬өг![]() Ј¬
Ј¬![]() ОӘЕЧОпПЯ
ОӘЕЧОпПЯ![]() ЙПөДБҪёц¶ҜөгЈЁ
ЙПөДБҪёц¶ҜөгЈЁ![]() ФЪ
ФЪ![]() өДЧуІаЈ©Ј¬ЗТ
өДЧуІаЈ©Ј¬ЗТ![]() ЦбЈ¬ТФ
ЦбЈ¬ТФ![]() ОӘұЯ»ӯҫШРО
ОӘұЯ»ӯҫШРО![]() Ј¬Фӯөг
Ј¬Фӯөг![]() ФЪұЯ
ФЪұЯ![]() ЙПЈ®
ЙПЈ®
ЈЁ1Ј©ИзНј1Ј¬өұҫШРО![]() ОӘХэ·ҪРОКұЈ¬ЗуёГҫШРОФЪөЪТ»ПуПЮДЪөДЖжМШөгөДЧшұкЈ®
ОӘХэ·ҪРОКұЈ¬ЗуёГҫШРОФЪөЪТ»ПуПЮДЪөДЖжМШөгөДЧшұкЈ®
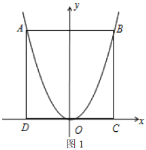
ЈЁ2Ј©ИзНј2Ј¬ФЪөг![]() Ј¬
Ј¬![]() өДФЛ¶Ҝ№эіМЦРЈ¬Б¬Ҫб
өДФЛ¶Ҝ№эіМЦРЈ¬Б¬Ҫб![]() Ҫ»ЕЧОпПЯУЪөг
Ҫ»ЕЧОпПЯУЪөг![]() Ј®
Ј®
ўЩЗуЦӨЈәөг![]() ОӘҫШРОөДЖжМШөгЈ»
ОӘҫШРОөДЖжМШөгЈ»
ўЪБ¬Ҫб![]() Ј¬Иф
Ј¬Иф![]() Ј¬ЕЧОпПЯЙПөДөг
Ј¬ЕЧОпПЯЙПөДөг![]() ОӘҫШРОөДБнТ»ЖжМШөгЈ¬Зуҫӯ№э
ОӘҫШРОөДБнТ»ЖжМШөгЈ¬Зуҫӯ№э![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ИэөгөДФІөД°лҫ¶Ј®
ИэөгөДФІөД°лҫ¶Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЎчABCөД¶ҘөгЧшұк·ЦұрОӘAЈЁ©Ғ6Ј¬0Ј©Ј¬BЈЁ4Ј¬0Ј©Ј¬CЈЁ0Ј¬8Ј©Ј¬°СЎчABCСШЦұПЯBC·ӯХЫЈ¬өгAөД¶ФУҰөгОӘDЈ¬ЕЧОпПЯy=ax2©Ғ10ax+cҫӯ№эөгCЈ¬¶ҘөгMФЪЦұПЯBCЙПЈ®

ЈЁ1Ј©ЦӨГчЛДұЯРОABCDКЗБвРОЈ¬ІўЗуөгDөДЧшұкЈ»
ЈЁ2Ј©ЗуЕЧОпПЯөД¶ФіЖЦбәНәҜКэұнҙпКҪЈ»
ЈЁ3Ј©ФЪЕЧОпПЯЙПКЗ·сҙжФЪөгPЈ¬К№өГЎчPBDУлЎчPCDөДГж»эПаөИЈҝИфҙжФЪЈ¬ЦұҪУРҙіцөгPөДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ·ҪіМ![]() өДёщҝЙКУОӘәҜКэ
өДёщҝЙКУОӘәҜКэ![]() өДНјПуУләҜКэ
өДНјПуУләҜКэ![]() өДНјПуҪ»өгөДәбЧшұкЈ¬Фт·ҪіМ
өДНјПуҪ»өгөДәбЧшұкЈ¬Фт·ҪіМ![]() өДКөёщ
өДКөёщ![]() ЛщФЪөД·¶О§КЗ(ЎЎЎЎ)
ЛщФЪөД·¶О§КЗ(ЎЎЎЎ)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬өгAФЪөЪТ»ПуПЮЈ¬BAЎНyЦбУЪөгBЈ¬·ҙұИАэәҜКэy=![]() ЈЁxЈҫ0Ј©өДНјПуУлПЯ¶ОABПаҪ»УЪөгCЈ¬ЗТCКЗПЯ¶ОABөДЦРөгЈ¬ИфЎчOABөДГж»эОӘ3Ј¬ФтkөДЦөОӘ( )
ЈЁxЈҫ0Ј©өДНјПуУлПЯ¶ОABПаҪ»УЪөгCЈ¬ЗТCКЗПЯ¶ОABөДЦРөгЈ¬ИфЎчOABөДГж»эОӘ3Ј¬ФтkөДЦөОӘ( )
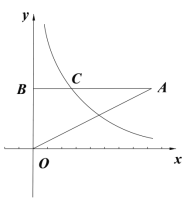
A.![]() B.1C.2D.3
B.1C.2D.3
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
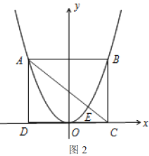
ЎҫМвДҝЎҝТСЦӘЈәИзНјўЩЈ¬ФЪҫШРОABCDЦРЈ¬AB=3Ј¬AD=4Ј¬AEЎНBDЈ¬ҙ№ЧгКЗEЈ®өгFКЗөгE№ШУЪABөД¶ФіЖөгЈ¬Б¬ҪУAFЎўBFЈ®
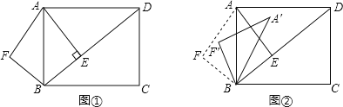
ЈЁ1Ј©ЗуAFәНBEөДіӨЈ»
ЈЁ2Ј©ИфҪ«ЎчABFСШЧЕЙдПЯBD·ҪПтЖҪТЖЈ¬ЙиЖҪТЖөДҫаАлОӘmЈЁЖҪТЖҫаАлЦёөгBСШBD·ҪПтЛщҫӯ№эөДПЯ¶ОіӨ¶ИЈ©Ј®өұөгF·ЦұрЖҪТЖөҪПЯ¶ОABЎўADЙПКұЈ¬ЦұҪУРҙіцПаУҰөДmөДЦөЈ®
ЈЁ3Ј©ИзНјўЪЈ¬Ҫ«ЎчABFИЖөгBЛіКұХлРэЧӘТ»ёцҪЗҰБЈЁ0ЎгЈјҰБЈј180ЎгЈ©Ј¬јЗРэЧӘЦРөДЎчABFОӘЎчAЎдBFЎдЈ¬ФЪРэЧӘ№эіМЦРЈ¬ЙиAЎдFЎдЛщФЪөДЦұПЯУлЦұПЯADҪ»УЪөгPЈ¬УлЦұПЯBDҪ»УЪөгQЈ®КЗ·сҙжФЪХвСщөДPЎўQБҪөгЈ¬К№ЎчDPQОӘөИСьИэҪЗРОЈҝИфҙжФЪЈ¬ЗуіцҙЛКұDQөДіӨЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
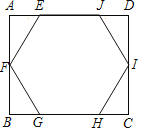
ЎҫМвДҝЎҝИзНјЈ¬ФЪҫШРОABCDЦРУРТ»ёцХэБщұЯРОEFGHIJЈ¬Жд¶ҘөгҫщФЪҫШРОөДұЯЙПЈ¬ұЯEJәНұЯGH·ЦұрФЪҫШРОөДұЯADәНBCЙПЈ¬Фт![]() ЈҪ_____Ј®
ЈҪ_____Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЛДұЯРОABCDКЗҫШРОЈ¬ADЎОxЦбЈ¬AЈЁ![]() Ј¬
Ј¬![]() Ј©Ј¬AB=1Ј¬AD=2Ј®
Ј©Ј¬AB=1Ј¬AD=2Ј®

ЈЁ1Ј©ЦұҪУРҙіцBЎўCЎўDИэөгөДЧшұкЈ»
ЈЁ2Ј©Ҫ«ҫШРОABCDПтУТЖҪТЖmёцөҘО»Ј¬К№өгAЎўCЗЎәГН¬КұВдФЪ·ҙұИАэәҜКэ![]() ЈЁ
ЈЁ![]() Ј©өДНјПуЙПЈ¬өГҫШРОAЎдBЎдCЎдDЎдЈ®ЗуҫШРОABCDөДЖҪТЖҫаАлmәН·ҙұИАэәҜКэөДҪвОцКҪЈ®
Ј©өДНјПуЙПЈ¬өГҫШРОAЎдBЎдCЎдDЎдЈ®ЗуҫШРОABCDөДЖҪТЖҫаАлmәН·ҙұИАэәҜКэөДҪвОцКҪЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com