
【题目】如图,直线AB,CD相交于O点,OM平分∠AOB.
(1)若∠1=∠2,求∠NOD的度数;
(2)若∠BOC=4∠1,求∠AOC与∠MOD的度数.

【答案】(1)90°;(2)∠AOC=60°;∠MON=150°.
【解析】
(1)根据角平分线的性质可得∠1+∠AOC=90°,再利用等量代换可得∠2+∠AOC=90°,利用邻补角互补可得答案;
(2)根据条件可得90°+∠1=4∠1,进而可得求出∠1=30°,从而可得∠AOC的度数,再利用邻补角互补可得∠MOD的度数.
(1)∵OM平分∠AOB,∴∠1+∠AOC=90°.
∵∠1=∠2,∴∠2+∠AOC=90°,∴∠NOD=180°﹣90°=90°;
(2)∵∠BOC=4∠1,∴90°+∠1=4∠1,∴∠1=30°,∴∠AOC=90°﹣30°=60°,∠MOD=180°﹣30°=150°.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法:①平角就是一条直线;②直线比射线线长;③平面内三条互不重合的直线的公共点个数有0个、1个、2个或3个;④连接两点的线段叫两点之间的距离;⑤两条射线组成的图形叫做角;⑥一条射线把一个角分成两个角,这条射线是这个角的角平分线,其中正确的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A(﹣1,0)、B(3,0),与y轴负半轴交于点C.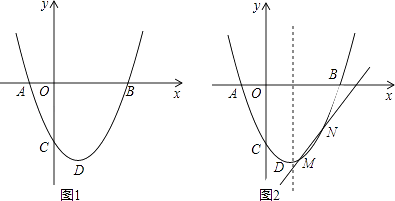
(1)若△ABD为等腰直角三角形,求此时抛物线的解析式;
(2)a为何值时△ABC为等腰三角形?
(3)在(1)的条件下,抛物线与直线y= ![]() x﹣4交于M、N两点(点M在点N的左侧),动点P从M点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点N,若使点P运动的总路径最短,求点P运动的总路径的长.
x﹣4交于M、N两点(点M在点N的左侧),动点P从M点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点N,若使点P运动的总路径最短,求点P运动的总路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为______.
的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱体铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上). 现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示.①图2中折线ABC表示___________槽中水的深度与注水时间之间的关系(选填“甲”或“乙”);②点B的纵坐标表示的实际意义是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在所给图形中:
⑴求证:∠BDC=∠A+∠B+∠C;
⑵如果点D与点A分别在线段BC的两侧,猜想∠BDC、∠A、∠B、∠C这4个角之间有怎样的关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com