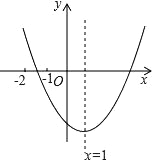
【题目】已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列结论：①b2﹣4ac＞0； ②abc＞0； ③8a+c＜0； ④9a+3b+c＞0．其中，正确结论的个数（ ）
A. 1B. 2C. 3D. 4
【答案】B
【解析】
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
①由图知：抛物线与x轴有两个不同的交点，则△＝b2﹣4ac＞0，故①正确；
②抛物线开口向上，得：a＞0；对称轴为x
1，则b＝﹣2a，故b＜0；
抛物线交y轴于负半轴，得：c＜0；
所以abc＞0；故②正确；
③观察图象得当x＝﹣2时，y＞0，即4a﹣2b+c＞0．
∵b＝﹣2a，∴4a+4a+c＞0，即8a+c＞0，故③错误；
④根据抛物线的对称轴方程可知：（﹣1，0）关于对称轴的对称点是（3，0）；
当x＝﹣1时，y＜0，所以当x＝3时，也有y＜0，即9a+3b+c＜0；故④错误；
综上所述：正确的说法是：①②．
故选B．
科目：初中数学 来源： 题型：
【题目】把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=4 cm，则球的半径长是（ ）
A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线
的对称轴是直线
，且过点（1，0）.顶点位于第二象限，其部分图像如图所示，给出以下判断：
①
且
；
②
；
③
；
④
；
⑤直线
与抛物线两个交点的横坐标分别为
，则
.其中正确的个数有( )
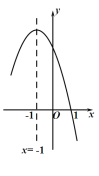
A. 5个B. 4个C. 3个D. 2个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于二次函数
和一次函数
，我们把 
称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图象记作抛物线E.现有点A(1,0)和抛物线E上的点B(2,n)，请完成下列任务：
（尝试）
（1）当t=2时，抛物线的顶点坐标为 .
（2）判断点A是否在抛物线E上；
（3）求n的值.
（发现）通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线E总过定点，定点的坐标 .
（应用）二次函数
是二次函数和一次函数 的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
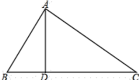
【题目】已知：如图，
中，
于
，下列条件：
；(2)∠B=∠DAC；(3)
= 
；(4)AB2=BD
BC.其中一定能够判定是直角三角形的有（ ）
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y=x
+bx+c，经过点A（0，5）和点B（3，2）
（1）求抛物线的解析式：
（2）现有一半径为l，圆心P在抛物线上运动的动圆，问⊙P在运动过程中，是否存在⊙P与坐标轴相切的情况？若存在，请求出圆心P的坐标：若不存在，请说明理由；
（3）若⊙Q的半径为r，点Q 在抛物线上、⊙Q与两坐轴都相切时求半径r的值
查看答案和解析>>
科目：初中数学 来源： 题型：
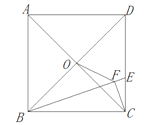
【题目】如图，正方形ABCD的边长为6，点O是对角线AC、BD的交点.点E在CD上，且DE=2CE，连接BE.过点C作CF⊥BE，垂足是F，连接OF，则OF的长为 .
查看答案和解析>>
科目：初中数学 来源： 题型：
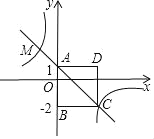
【题目】如图，四边形ABCD为正方形，点A坐标为（0，1），点B坐标为（0，﹣2），反比例函数y＝
的图象经过点C，一次函数y＝ax+b的图象经过A、C两点．
（1）求反比例函数与一次函数的解析式；
（2）若点P是反比例函数图象上的一点，△OAP的面积恰好等于正方形ABCD的面积，求P点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y=ax2+bx+c（0＜2a≤b）与x轴最多有一个交点．以下四个结论：
①abc＞0；
②该抛物线的对称轴在x=﹣1的右侧；
③关于x的方程ax2+bx+c+1=0无实数根；
④
≥2．
其中，正确结论的个数为（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com