
【题目】已知:如图,![]() 中,
中,![]() 于
于![]() ,下列条件:
,下列条件:![]() ;(2)∠B=∠DAC;(3)
;(2)∠B=∠DAC;(3)![]() =
= ![]() ;(4)AB2=BD
;(4)AB2=BD![]() BC.其中一定能够判定
BC.其中一定能够判定![]() 是直角三角形的有( )
是直角三角形的有( )
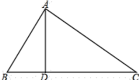
A. 0个B. 1个C. 2个D. 3个
【答案】D
【解析】
对题干中给出的条件逐一验证,证明∠BAC=90°即可解题.
解:(1)∵AD⊥BC,
∴∠B+∠BAD=90°,
∵∠B+∠DAC=90°,
∴∠BAD=∠DAC,
∴该条件无法判定△ABC是直角三角形;
(2)∵∠B=∠DAC,∠BAD+∠B=90°,
∴∠BAD+∠DAC=90°,
即∠BAC=90°,
故该条件可以判定△ABC是直角三角形;
(3)![]() =
= ![]() ,则△ADC∽△BDA,
,则△ADC∽△BDA,
∴∠CAD=∠ABD,
又∵∠ABD+∠BAD=90°,
∴∠BAD+∠CAD=90°,
∴该条件可以判定△ABC是直角三角形;
(4)∵AB2=BDBC,
![]()
∵∠B=∠B,
∴△ABD∽△CBA,
∴∠BAC=90°,
故该条件可以判定△ABC是直角三角形;
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应学习任务
旋转对称
把正n边形绕着它的中心旋转![]() 的整数倍后所得的正n边形重合.我们说,正n边形关于其中心有
的整数倍后所得的正n边形重合.我们说,正n边形关于其中心有![]() 的旋转对称.一般地,如果一个图形绕着某点O旋转角α(0<α<360°)后所得到的图形与原图形重合,则称此图形关于点O有角α的旋转对称.图1就是具有旋转对称性质的一些图形.
的旋转对称.一般地,如果一个图形绕着某点O旋转角α(0<α<360°)后所得到的图形与原图形重合,则称此图形关于点O有角α的旋转对称.图1就是具有旋转对称性质的一些图形.

任务:
(1)如图2,正六边形关于其中心O有 的旋转对称,中心对称图形关于其对称中心有 的旋转对称;
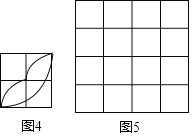
(2)图3是利用旋转变换设计的具有旋转对称性的一个图形,将该图形绕其中心至少旋转 与原图形重合;
(3)请以图4为基本图案,在图5中利用平移、轴对称或旋转进行图案设计,使得设计出的图案是中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
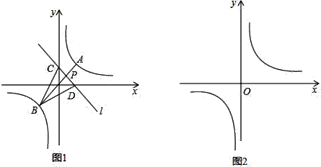
【题目】如图,点![]() 在反比例函数
在反比例函数![]() 第一象限的图象上,连接
第一象限的图象上,连接![]() ,延长
,延长![]() 与双曲线的另一支交于点
与双曲线的另一支交于点![]() ,作
,作![]() 的垂直平分线
的垂直平分线![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)在图![]() 中,当
中,当![]() ,直接写出
,直接写出![]() ,
,![]() ,
,![]() 三点的坐标,并求出直线
三点的坐标,并求出直线![]() 的解析式.
的解析式.
(2)当点![]() 的坐标为
的坐标为![]() 时,利用图
时,利用图![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象过点
的图象过点![]() 和点
和点![]() ,对称轴为直线
,对称轴为直线![]() .
.

![]() 求该二次函数的关系式和顶点坐标;
求该二次函数的关系式和顶点坐标;
![]() 结合图象,解答下列问题:
结合图象,解答下列问题:
①当![]() 时,求函数
时,求函数![]() 的取值范围.
的取值范围.
②当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
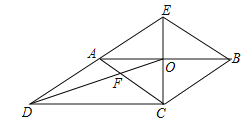
【题目】如图,CE是ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:
①四边形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
④S四边形AFOE:S△COD=2:3.
其中正确的结论有_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2﹣4ac>0; ②abc>0; ③8a+c<0; ④9a+3b+c>0.其中,正确结论的个数( )
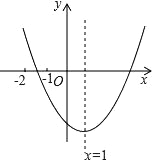
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有4张卡片.4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子任意抽取一张卡片,恰好抽到标有奇数卡片的概率是: ;
(2)先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2张卡片标有数字之和大于4的概率(请用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒.
(1)当t=2时,求点E的坐标;
(2)若AB平分∠EBP时,求t的值.
(3)在运动的过程中,是否存在以P、O、E为顶点的三角形与△ABE相似.若存在,请求出点P的坐标;若不存在,请说明理由.
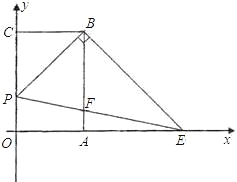
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣![]() 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为__.
上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com