
根据指令[s, A](s≥0,0°<A≤360°),机器人在平面上完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向行走s个单位.现机器人在平面直角坐标系的原点,且面对x轴的正方向,如果输入
A](s≥0,0°<A≤360°),机器人在平面上完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向行走s个单位.现机器人在平面直角坐标系的原点,且面对x轴的正方向,如果输入
 指令为[1,45°],那么连续执行三次这样的指令,机器人
指令为[1,45°],那么连续执行三次这样的指令,机器人 所在位置的坐标是( )
所在位置的坐标是( )
A.(0, ) B.(
) B.( ,
, )
) C.(
C.( ,
, ) D.(0,1+
) D.(0,1+ )
)
科目:初中数学 来源: 题型:
如图,矩形ABCD中,AB=3,BC=4,将矩形ABCD沿对角线AC平移,平移后的矩形为EFGH(A、E、C、G始终在同一条直线上),当点E与C重合时停止移动.平移中EF与BC交 于点N,GH与BC的延长线交于点M,EH与DC交于点P,FG与DC的延长线交于点Q.设S表示矩形PCMH的面积,
于点N,GH与BC的延长线交于点M,EH与DC交于点P,FG与DC的延长线交于点Q.设S表示矩形PCMH的面积,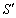
 表
表 示矩形NFQC的面积
示矩形NFQC的面积
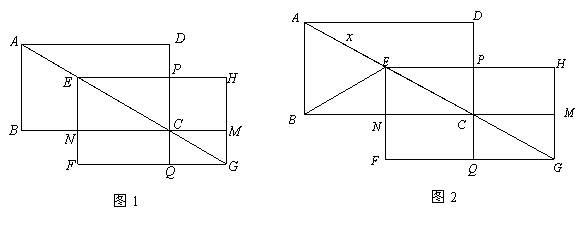

(1)S与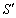
 吗?请说明理由.
吗?请说明理由.
(2)设AE=x,写出S和x之间的函数关系式,并求出x取何值时S有最大值,最 大值是多少?
大值是多少?
(3)如图2,连结BE,当AE为何值时,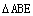
 是
是 等腰三角形.
等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
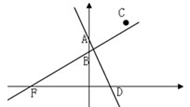
已知在直角坐标系中,A(0,2),F(-3,0),D为x轴上一动点,过点F作直线AD的 垂线FB,交y轴于B,点C(2,
垂线FB,交y轴于B,点C(2,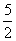
 )为定点,在点D移动的过程中,如果以A,B,C,D为顶点的四边形是梯形,则点D的坐标为_______________.
)为定点,在点D移动的过程中,如果以A,B,C,D为顶点的四边形是梯形,则点D的坐标为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,矩形MNPQ中,点E 、F、G、H分别在NP、PQ、QM、MN上,若
、F、G、H分别在NP、PQ、QM、MN上,若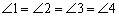
 ,则称四边形EF
,则称四边形EF GH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且
GH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且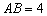
 ,
,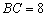
 .
.
(1)在图2、图3中,点E、F分别在BC、CD边上,图 2中的四边形EFGH是利用正方形网格在图上画出的矩形ABCD的反射四边形.请你利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH;
2中的四边形EFGH是利用正方形网格在图上画出的矩形ABCD的反射四边形.请你利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH;
(2)图2、图3中矩形ABCD的反射四边形EFGH的周长是否为定值?若是定值,请直接写出这个定值;若不是定值,请直接写出图2、图3中矩形ABCD的反射四边形EFGH的周长各是多少;
(3)图2、图3中矩形ABCD的反射四边形EFGH的面积是否为定值?若是定值,请直接写出这个定值;若不是定 值,请直接写出图2、图3中矩形ABCD的反射四边形E
值,请直接写出图2、图3中矩形ABCD的反射四边形E FGH的面积各是多少.
FGH的面积各是多少.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,平面直角坐标系中,点B(0,2),以B为圆心, 1为半径作圆,把⊙B沿着直线y = x方
1为半径作圆,把⊙B沿着直线y = x方 向
向 平移,当平移的距离为__________
平移,当平移的距离为__________ 时,⊙B与x轴相切。
时,⊙B与x轴相切。


查看答案和解析>>
科目:初中数学 来源: 题型:
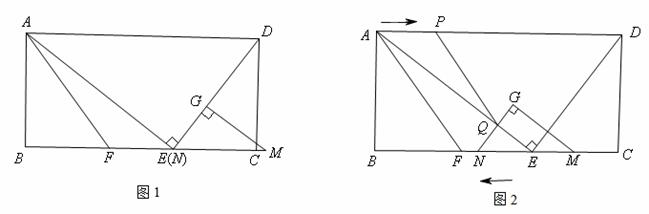
已知:在矩形ABCD中,E 为
为 边BC上的一点,AE⊥DE,AB=12,BE=
边BC上的一点,AE⊥DE,AB=12,BE=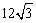 ,F为线段BE上一点,EF=7,连接AF。如图1,现有一张硬纸片△GMN,∠NGM=900,NG=6,MG=
,F为线段BE上一点,EF=7,连接AF。如图1,现有一张硬纸片△GMN,∠NGM=900,NG=6,MG=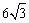 ,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上。如图2,△GMN从图1的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点
,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上。如图2,△GMN从图1的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点 出发,以每秒2个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ。当点G到达线段AE上时,△GMN和点P同时停止运动。设运动时间为t秒,解答问题:
出发,以每秒2个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ。当点G到达线段AE上时,△GMN和点P同时停止运动。设运动时间为t秒,解答问题:
(1)在整个运动过程中,当点G在线段AE上时,求t的值;
(2)在整个运动过程中,是否存在点P,使△APQ是直角三角形,若存在,求出t的值;若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com