
如图,平面直角坐标系中,点B(0,2),以B为圆心, 1为半径作圆,把⊙B沿着直线y = x方
1为半径作圆,把⊙B沿着直线y = x方 向
向 平移,当平移的距离为__________
平移,当平移的距离为__________ 时,⊙B与x轴相切。
时,⊙B与x轴相切。


科目:初中数学 来源: 题型:
两个全等的梯形纸片如图(1)摆放,将梯形纸片ABCD沿上底AD方向向右平移得到图(2).已知AD=4,BC=8,若 阴影部分的面积等于四边形A′B′BA的面积,则图(2)中平移距离A′A= .
阴影部分的面积等于四边形A′B′BA的面积,则图(2)中平移距离A′A= .

查看答案和解析>>
科目:初中数学 来源: 题型:
在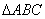
 中,
中,
 现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿A
现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿A C向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E,连结EQ。设动点运动时间为x秒。
C向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E,连结EQ。设动点运动时间为x秒。


(1)用含x的代数式表示AE、DE的长度;
(2)当点Q在BD(不包括点 B、D)上移动时,设
B、D)上移动时,设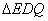
 的面积为
的面积为
 ,求
,求
 与月份
与月份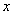
 的函数关
的函数关 系式,并写出自变量
系式,并写出自变量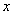
 的取值范围;
的取值范围;
(3)当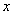
 为何值时,
为何值时,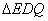
 为直角三角形。
为直角三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线l1与x轴、y轴分别交于A、B两点,直线l2与直线l1关于x轴对称,已知直线l1的解析式为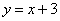
 .
.


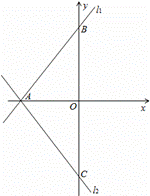

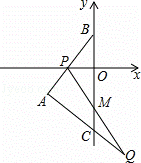

(1) 求直线l2的解析式;
求直线l2的解析式;
(2)过A点在△ABC的外部作一条直线l3,过点B作BE⊥l3于E,过点C作CF⊥l3于F,请画出图形并求证:BE+CF=EF;
(3)△ABC沿y轴向下平移,AB边交x轴于点P,过P点的直线与AC边的延长线相交于点Q,与y轴相交于点M,且BP=CQ,在△ABC平移的过程中,①OM为定值;②MC为定值.在这两个结论中,有且只有一个是正确的,请找出正确的结论,并求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
根据指令[s, A](s≥0,0°<A≤360°),机器人在平面上完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向行走s个单位.现机器人在平面直角坐标系的原点,且面对x轴的正方向,如果输入
A](s≥0,0°<A≤360°),机器人在平面上完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向行走s个单位.现机器人在平面直角坐标系的原点,且面对x轴的正方向,如果输入
 指令为[1,45°],那么连续执行三次这样的指令,机器人
指令为[1,45°],那么连续执行三次这样的指令,机器人 所在位置的坐标是( )
所在位置的坐标是( )
A.(0, ) B.(
) B.( ,
, )
) C.(
C.( ,
, ) D.(0,1+
) D.(0,1+ )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF.

(1)如图1,若点G是边BC的中点,连接FG,则EF与FG关系为: ;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转900,得到线段FQ,连接EQ,请猜想EF、EQ、BP三者之间的数量关系,并证明你的结论;
(3)若点P为CB延长线上一动点,按照(2)中的作法,在图3中补全 图形,并直接写出EF、EQ、BP三者之间的数量关系: .
图形,并直接写出EF、EQ、BP三者之间的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角 梯形,其中三边长分别为2、2、3,则原直角三角形纸片
梯形,其中三边长分别为2、2、3,则原直角三角形纸片 的斜边长是 。
的斜边长是 。
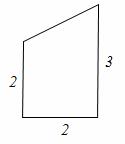
查看答案和解析>>
科目:初中数学 来源: 题型:
对于 实数x,我们规定
实数x,我们规定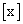 表示不大于x的
表示不大于x的 最大整数,如
最大整数,如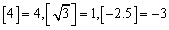 ,现对82进行如下操作:
,现对82进行如下操作: ,这样对82只需进行
,这样对82只需进行 3次操作后变
3次操作后变 为1,类似地,①对121只需进行 次操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是
为1,类似地,①对121只需进行 次操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com