
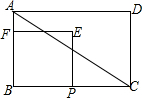
 如图,在矩形ABCD中,AB=6,BC=8,点P从点B出发以每秒2个单位长度的速度向终点C运动,点P不与点B重合,以BP为边在BC上方作正方形BPEF,设正方形BPEF与△ABC的重叠部分图形的面积为S(平方单位),点P的运动时间为t(秒).
如图,在矩形ABCD中,AB=6,BC=8,点P从点B出发以每秒2个单位长度的速度向终点C运动,点P不与点B重合,以BP为边在BC上方作正方形BPEF,设正方形BPEF与△ABC的重叠部分图形的面积为S(平方单位),点P的运动时间为t(秒).分析 (1)根据PC=BC-BP可得出PC长度关于t的表达式,结合PC≥0即可得出t的取值范围;
(2)当点P落在线段AC上时,由正方形的性质可得知EP∥AB,由此得出△CPE∽△CBA,根据相似三角形的相似比即可得出结论;
(3)随着点P的运动,按正方形BPEF与△ABC的重叠部分图形的形状不同分情况考虑:①为正方形时,结合(2)结论可得知此时t的取值范围,由正方形的面积公式即可得出S关于t的函数关系式;②为五边形时,由F点在线段AB上可得出此时t的取值范围,根据S=大三角形面积-2个小三角形的面积即可得出S关于t的函数关系式;③为梯形时,t为值域内剩下的部分,根据S=大三角形面积-小三角形面积即可得出S关于t的函数关系式;
(4)按运动的过程寻找,找出几个临界点,求出此时的t值,结合实际情况即可得出结论.
解答 解:(1)BP=2t,PC=BC-BP=8-2t,
∵$\left\{\begin{array}{l}{2t>0}\\{8-2t≥0}\end{array}\right.$,
∴0<t≤4.
故PC=-2t+8(0<t≤4).
(2)当点P落在线段AC上时,
∵EP∥AB,
∴△CPE∽△CBA,
∴$\frac{EP}{AB}=\frac{PC}{BC}$,即$\frac{2t}{6}=\frac{8-2t}{8}$,
解得:t=$\frac{12}{7}$.
(3)按P点运动的过程中正方形BPEF与△ABC的重叠部分图形的形状不同分3种情况考虑: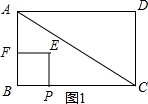
①当0<t≤$\frac{12}{7}$时,如图1所示.
此时S=BP2=(2t)2=4t2;
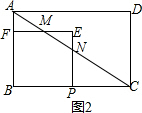
②当$\frac{12}{7}$<t≤3时,如图2所示.
此时BF=BP=2t,PC=8-2t,AF=6-2t,
∵NP∥AB,FM∥BC,
∴△CNP∽△CAB∽△MAF,
∴$\frac{PC}{NP}=\frac{BC}{AB}=\frac{FM}{AF}$,
∴NP=$\frac{3}{4}$PC=6-$\frac{3}{2}$t,FM=$\frac{4}{3}$AF=8-$\frac{8}{3}$t.
S=$\frac{1}{2}$BC•AB-$\frac{1}{2}$PC•NP-$\frac{1}{2}$FM•AF=$\frac{1}{2}$×6×8-$\frac{1}{2}$(8-2t)(6-$\frac{3}{2}$t)-$\frac{1}{2}$(8-$\frac{8}{3}$t)(6-2t)=-$\frac{25}{6}{t}^{2}$+28t-24;
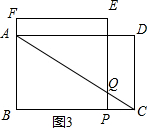
③当3<t≤4时,如图3所示.
∵PQ∥AB,
∴△CPQ∽△CBA,
∴$\frac{PQ}{PC}=\frac{BA}{BC}$,
∴PQ=$\frac{3}{4}$PC=6-$\frac{3}{2}$t.
S=$\frac{1}{2}$BC•AB-$\frac{1}{2}$PC•PQ=$\frac{1}{2}$×8×6-$\frac{1}{2}$(8-2t)(6-$\frac{3}{2}$t)=-$\frac{3}{2}$t2+12t.
(4)根据P点的运动,画出正方形OC′MN与△ACD重叠部分图形为三角形时的临界点.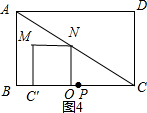
①当P点开始往右移动时,正方形OC′MN与△ACD重叠部分图形为三角形,达到图4所示情况时不再为三角形.
此时:OC′=ON,
∵点O为线段BC的中点,ON∥AB,
∴ON为△CAB的中位线,
∴OC′=ON=$\frac{1}{2}$AB=3,
CC′=OC′+OC=3+4=7,
∴PC=$\frac{1}{2}$CC′=$\frac{7}{2}$=8-2t,
解得:t=$\frac{9}{4}$.
即0<t<$\frac{9}{4}$;
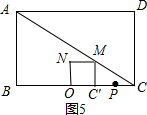
②当P点运动到图5所示情况时,正方形OC′MN与△ACD重叠部分图形开始为三角形.
此时MC′=$\frac{3}{4}$CC′=OC′,OC=OC′+CC′=4,
∴MC′=$\frac{12}{7}$,CC′=$\frac{16}{7}$,
∴PC=$\frac{1}{2}$CC′=$\frac{8}{7}$=8-2t,
解得:t=$\frac{24}{7}$;
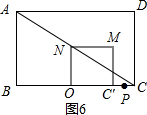
③当P点运动到图6所示情况,正方形OC′MN与△ACD重叠部分图形为三角形,P再运动一点时不再为三角形.
此时OC′=ON=$\frac{1}{2}$AB=3,CC′=OC-OC′=4-3=1,
∴PC=$\frac{1}{2}$CC′=$\frac{1}{2}$=8-2t,
解得:t=$\frac{15}{4}$.
综上知:当正方形OC′MN与△ACD重叠部分图形为三角形时,t的取值范围为0<t<$\frac{9}{4}$和$\frac{24}{7}$<t≤$\frac{15}{4}$.
点评 本题考查了相似三角形的判定及性质、解一元一次方程、一元一次不等式组以及三角形的面积公式,解题的关键是:(1)根据不等式组找出t的取值范围;(2)找出比例关系;(3)根据重合图形的不同分类讨论;(4)按P点的运动过程寻找临界点.本题属于中档题,难度不小,题中出现大量图形,深刻的体现了数形结合的重要性.


科目:初中数学 来源: 题型:解答题
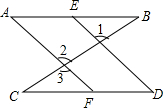 已知:如图,∠B=∠C,∠1=∠3.求证:∠A=∠D.
已知:如图,∠B=∠C,∠1=∠3.求证:∠A=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
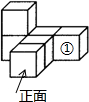 如图是由6个同样大小的正方体搭成的立体图形,将正方体①移走后,所得立体图形( )
如图是由6个同样大小的正方体搭成的立体图形,将正方体①移走后,所得立体图形( )| A. | 主视图改变,左视图改变 | B. | 俯视图不变,左视图不变 | ||
| C. | 俯视图改变,左视图改变 | D. | 主视图改变,左视图不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
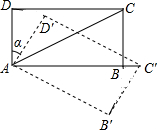 如图,在长方形ABCD中,AB=$\sqrt{3}$,AD=1,该长方形绕点A顺时针旋转α度得长方形AB′C′D′,点C′落在AB的延长线上,则线段BC′的长是2-$\sqrt{3}$.
如图,在长方形ABCD中,AB=$\sqrt{3}$,AD=1,该长方形绕点A顺时针旋转α度得长方形AB′C′D′,点C′落在AB的延长线上,则线段BC′的长是2-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
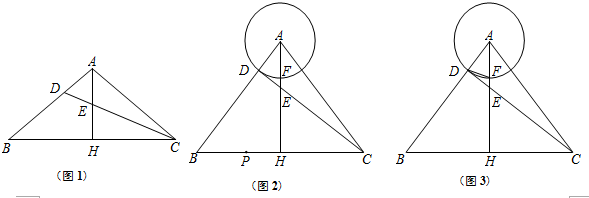
 如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.
如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{12}$÷$\sqrt{3}$=2 | C. | $\sqrt{6}$×(-$\sqrt{3}$)=3$\sqrt{2}$ | D. | ($\sqrt{3}$-1)2=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com