

分析 (1)由矩形的性质得到OA=OC,AD∥BC从而得出△AOE≌△COF,即可;
(2)由矩形的性质和菱形的性质得出线段的关系,利用勾股定理建立方程16+x2=(6-x)2,即可;
(3)由对折的性质得出线段和角相等,判断出角相等,从而判断A′B∥C′D,利用一组对边平行且相等的四边形是平行四边形,即可;
(4)由A′C′最短,只有点A′,C′在线段EF上,计算即可.
解答 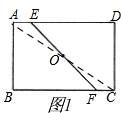
(1)证明:如图1,连接AC,
∴点O在线段AC上,AD∥BC,OA=OC,
∴∠AOE=∠COF,∠EAO=∠FCO,
∴△AOE≌△COF,
∴AE=CF;
(2)解:如图2,连接BD,
∵四边形ABCD为矩形,
∴AB=CD,∠BAE=∠DCF,
由(1)有AE=CF,
∴DE=BF
Rt△ABE≌Rt△CDF,
∴BE=DF,
∵EF=EF,
∴四边形BEDF是平行四边形.
设AE=x,则DE=6-x,
∵四边形BEDF是菱形,
∴BE=BD=6-x,
在Rt△ABE中,AB=4,
根据勾股定理,得 AB2+AE2=BE2,
∴16+x2=(6-x)2,
∴x=$\frac{5}{3}$.
故答案为平行四边形,$\frac{5}{3}$.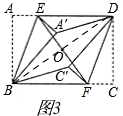
(3)解:如图3,连接BD,由(1)有,AE=CF,
∵四边形ABCD为矩形,
∴∠A=∠C=90°,AB=CD,AB∥CD,
∴Rt△ABE≌Rt△CDF,
∴∠ABE=CDF,
∵沿BE翻折,点A落在A′处,
∴Rt△ABE≌Rt△A′BE,
∴A′B=AB,∠ABE=∠A′BE=$\frac{1}{2}$∠ABA′
同理可得,C′D=CD,∠CDF=∠C′DF=$\frac{1}{2}$∠C′DC,
∴∠ABA′=∠C′DC,A′B=C′D,
∠ABO-∠ABA′=∠CDO-∠CDC′,
∴∠OBA′=∠ODC′,
∴A′B∥C′D,
∴四边形BA′DC′是平行四边形;
(4)解:由(3)可知,A'C'=2OA',
∴A'C'最小时,OA'最小.
连接OB,在△A'OB中,
OA'≥A'B-OB,
∴OA'取最小值时,点B,O,A'共线;
即落在对角线上.
∴要使A′C′最小,只有点A′,C′落在矩形对角线BD上,
设AE=x,
∴EA′=x,DE=6-x,矩形的对角线BD=$\sqrt{{BC}^{2}{+CD}^{2}}$=2$\sqrt{13}$,
由对折有BA′=BA=4
∴DA′=BD-BA′=2$\sqrt{13}$-4,
在Rt△DEA′中,有DE2=EA′2+DA′2,
∴(6-x)2=x2+(2$\sqrt{13}$-4)2
∴x=$\frac{4\sqrt{13}-8}{3}$,
即:AE=$\frac{4\sqrt{13}-8}{3}$.
点评 本题是四边形的综合题,主要考查了四边形中的平行四边形和矩形的性质和判定,涉及到的知识点还有对折,三角形的全等,勾股定理,解本题的关键是判断三角形全等和对折的性质,本题的难点是作辅助线.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
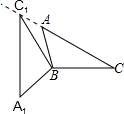 如图,在△ABC中,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1,当点C1在线段CA的延长线上时,则∠CC1A1=60°.
如图,在△ABC中,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1,当点C1在线段CA的延长线上时,则∠CC1A1=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
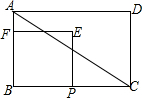 如图,在矩形ABCD中,AB=6,BC=8,点P从点B出发以每秒2个单位长度的速度向终点C运动,点P不与点B重合,以BP为边在BC上方作正方形BPEF,设正方形BPEF与△ABC的重叠部分图形的面积为S(平方单位),点P的运动时间为t(秒).
如图,在矩形ABCD中,AB=6,BC=8,点P从点B出发以每秒2个单位长度的速度向终点C运动,点P不与点B重合,以BP为边在BC上方作正方形BPEF,设正方形BPEF与△ABC的重叠部分图形的面积为S(平方单位),点P的运动时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
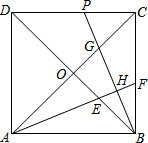 已知正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于点E、F,作BH⊥AF,垂足为H,BH的延长线分别交AC、CD于点G、P.
已知正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于点E、F,作BH⊥AF,垂足为H,BH的延长线分别交AC、CD于点G、P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com