Question

9．如图1，在4×8的网格纸中，每个小正方形的边长都为1，动点P、Q分别从点D、A同时出发向右移动，点P的运动速度为每秒1个单位，点Q的运动速度为每秒0.5个单位，当点P运动到点C时，两个点都停止运动，设运动时间为t（0＜t＜8）．
（1）请在4×8的网格纸图2中画出t为6秒时的线段PQ．并求其长度； 
（2）当t为多少时．△PQB是以BP为底的等腰三角形．

Answer 1

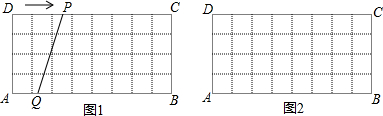
分析 （1）根据点P的运动速度为每秒1个单位，点Q的运动速度为每秒0.5个单位可知，当t=6秒时，DP=6，AQ=3即可画出线段PQ；
（2）设时间为t，则在t秒钟，P运动了t个单位，Q运动了$\frac{1}{2}$t个单位，由题意得 PQ=BQ，然后根据勾股定理列出关于t的方程，解得t即可．

解答 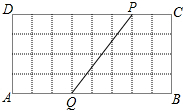解：（1）如图所示，由勾股定理得PQ=$\sqrt{{3}^{2}+{4}^{2}}$=5；

（2）设时间为t，则在t秒钟，P运动了t格，Q运动了$\frac{1}{2}$t格，由题意得PQ=BQ，
即（t-$\frac{1}{2}$t）²+4²=（8-$\frac{1}{2}$t）²，解得t=6（秒）．
答：当t为6秒时．△PQB是以BP为底的等腰三角形．

点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．